题目内容
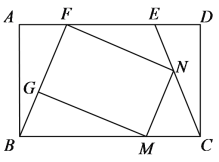
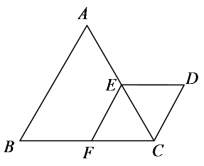
【题目】如图,△ABC与△CDE都是等边三角形,点E、F分别在AC、BC上,且EF∥AB.
(1)求证:四边形EFCD是菱形;
(2)设CD=2,求D、F两点间的距离.
【答案】(1)见解析;(2)![]()
【解析】
(1)由等边三角形的性质得出ED=CD=CE,证出△CEF是等边三角形,得出EF=CF=CE,得出ED=CD=EF=CF,即可得出结论;
(2)连接DF,与CE相交于点G,根据菱形的性质求出DG,即可得出结果.
(1)证明:∵△ABC与△CDE都是等边三角形,
∴ED=CD=CE,∠A=∠B=∠BCA=60°.
∴EF∥AB.
∴∠CEF=∠A=60°,∠CFE=∠B=60°,
∴∠CEF=∠CFE=∠ACB,
∴△CEF是等边三角形,
∴EF=CF=CE,
∴ED=CD=EF=CF,
∴四边形EFCD是菱形.
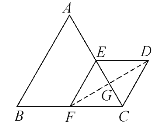
(2)连接DF与CE交于点G
∵四边形EFCD是菱形
∴DF⊥CE, DF=2DG
∵CD=2,△EDC是等边三边形
∴CG=1,DG=![]()
∴DF=2DG=![]() ,即D、F两点间的距离为
,即D、F两点间的距离为![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目