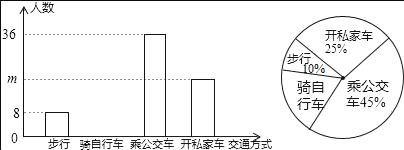
题目内容
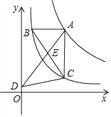
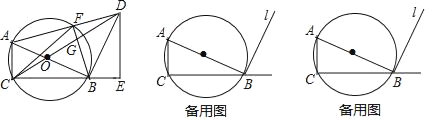
【题目】如图,⊙O是Rt△ABC的外接圆,∠C=90°,tanB=![]() ,过点B的直线l是⊙O的切线,点D是直线l上一点,过点D作DE⊥CB交CB延长线于点E,连接AD,交⊙O于点F,连接BF、CD交于点G.
,过点B的直线l是⊙O的切线,点D是直线l上一点,过点D作DE⊥CB交CB延长线于点E,连接AD,交⊙O于点F,连接BF、CD交于点G.
(1)求证:△ACB∽△BED;
(2)当AD⊥AC时,求![]() 的值;
的值;
(3)若CD平分∠ACB,AC=2,连接CF,求线段CF的长.
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)只要证明∠ACB=∠E,∠ABC=∠BDE即可;
(2)首先证明BE:DE:BC=1:2:4,由△GCB∽△GDF,可得![]() =
=![]() ;
;
(3)想办法证明AB垂直平分CF即可解决问题.
(1)证明:如图1中,
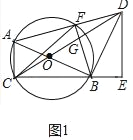
∵DE⊥CB,
∴∠ACB=∠E=90°,
∵BD是切线,
∴AB⊥BD,
∴∠ABD=90°,
∴∠ABC+∠DBE=90°,∠BDE+∠DBE=90°,
∴∠ABC=∠BDE,
∴△ACB∽△BED;
(2)解:如图2中,

∵△ACB∽△BED;四边形ACED是矩形,
∴BE:DE:BC=1:2:4,
∵DF∥BC,
∴△GCB∽△GDF,
∴![]() =
=![]() ;
;
(3)解:如图3中,
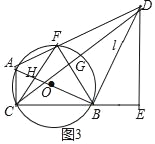
∵tan∠ABC=![]() =
=![]() ,AC=2,
,AC=2,
∴BC=4,BE=4,DE=8,AB=2![]() ,BD=4
,BD=4![]() ,
,
易证△DBE≌△DBF,可得BF=4=BC,
∴AC=AF=2,
∴CF⊥AB,设CF交AB于H,
则CF=2CH=2×![]() .
.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目