题目内容
【题目】已知:线段![]() ,以
,以![]() 为公共边,在
为公共边,在![]() 两侧分别作
两侧分别作![]() 和
和![]() ,并使
,并使![]() .点
.点![]() 在射线
在射线![]() 上.
上.
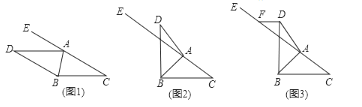
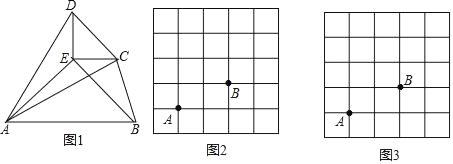
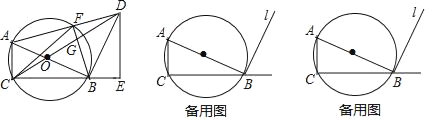
(1)如图l,若![]() ,求证:
,求证:![]() ;
;
(2)如图2,若![]() ,请探究
,请探究![]() 与
与![]() 的数量关系,写出你的探究结论,并加以证明;
的数量关系,写出你的探究结论,并加以证明;
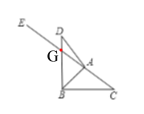
(3)如图3,在(2)的条件下,若![]() ,过点
,过点![]() 作
作![]() 交射线于点
交射线于点![]() ,当
,当![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)见详解;(2)![]() +2
+2![]() =90°,理由见详解;(3)99°.
=90°,理由见详解;(3)99°.
【解析】
(1)根据平行线的性质和判定定理,即可得到结论;
(2)设CE与BD交点为G,由三角形外角的性质得∠CGB=∠D+∠DAE,由![]() ,得∠CGB+∠C=90°,结合
,得∠CGB+∠C=90°,结合![]() ,即可得到结论;
,即可得到结论;
(3)设∠DAE=x,则∠DFE=8x,由![]() ,
,![]() +2
+2![]() =90°,得关于x的方程,求出x的值,进而求出∠C,∠ADB的度数,结合∠BAD=∠BAC,即可求解.
=90°,得关于x的方程,求出x的值,进而求出∠C,∠ADB的度数,结合∠BAD=∠BAC,即可求解.
(1)∵![]() ,
,
∴∠C+∠CBD=180°,
∵![]() ,
,
∴∠D+∠CBD=180°,
∴![]() ;
;
(2)![]() +2
+2![]() =90°,理由如下:
=90°,理由如下:
设CE与BD交点为G,
∵∠CGB是ADG的外角,
∴∠CGB=∠D+∠DAE,
∵![]() ,
,
∴∠CBD=90°,
∴在BCG中,∠CGB+∠C=90°,
∴∠D+∠DAE+∠C=90°,
又∵![]() ,
,
∴![]() +2
+2![]() =90°;
=90°;
(3)设∠DAE=x,则∠DFE=8x,
∴∠AFD=180°-8x,
∵![]() ,
,
∴∠C=∠AFD=180°-8x,
又∵![]() +2
+2![]() =90°,
=90°,
∴x+2(180°-8x)=90°,解得:x=18°,
∴∠C=180°-8x=36°=∠ADB,
又∵∠BAD=∠BAC,
∴∠ABC=∠ABD=![]() ∠CBD=45°,
∠CBD=45°,
∴∠BAD=180°-45°-36°=99°.

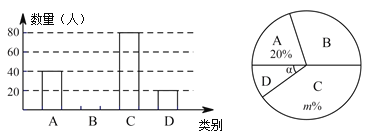
【题目】观察表格:根据表格解答下列问题:
x | 0 | 1 | 2 |
ax2 | 0 | 1 | 4 |
ax2+bx+c | ﹣3 | -4 | ﹣3 |
(l)求a,b,c的值;
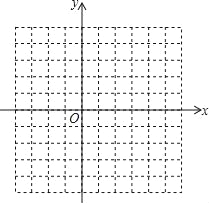
(2)在如图的直角坐标系中画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>﹣3成立;
(3)该图象与x轴两交点从左到右依次分别为A、B,与y轴交点为C,求过这三个点的外接圆的半径.