题目内容
平行四边形ABCD中,AB=6cm,BC=8cm,对角线AC、BD相交于点O,则:
小题1:①△BCO与△ABO的周长之差为 ;
小题2:②其对角线BD的长的取值范围是 。
小题1:①△BCO与△ABO的周长之差为 ;
小题2:②其对角线BD的长的取值范围是 。
小题1:2cm
小题2:
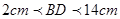
本题可先画出图形,根据三角形的周长公式以及平行四边形的性质,知:△BCO与△ABO的周长之差即为BC与AB的差;
根据平行四边形的性质,结合三角形的三边关系“第三边大于两边之差,而小于两边之和”,就可求得对角线的取值范围.
解:①∵四边形ABCD是平行四边形,

∴OA=OC.
又△BOC的周长=8+BO+CO,
△ABO的周长=6+AO+BO=6+CO+BO,
∴△BCO与△ABO的周长之差为8-6=2(cm);
②∵四边形ABCD是平行四边形,
∴CD=AB=6.
∴8-6<BD<8+6,
即2<BD<14.
故答案为2cm<BD<14cm.
本题考查了三角形的三边关系和平行四边形的性质.
平行四边形对边相等,对角线互相平分;
三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.
根据平行四边形的性质,结合三角形的三边关系“第三边大于两边之差,而小于两边之和”,就可求得对角线的取值范围.
解:①∵四边形ABCD是平行四边形,

∴OA=OC.
又△BOC的周长=8+BO+CO,
△ABO的周长=6+AO+BO=6+CO+BO,
∴△BCO与△ABO的周长之差为8-6=2(cm);
②∵四边形ABCD是平行四边形,
∴CD=AB=6.
∴8-6<BD<8+6,
即2<BD<14.
故答案为2cm<BD<14cm.
本题考查了三角形的三边关系和平行四边形的性质.
平行四边形对边相等,对角线互相平分;
三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.

练习册系列答案
相关题目
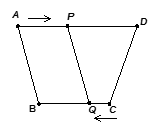

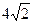 cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。
cm,∠C=45°,点P从B点出发,沿着BC方向以1cm/s运动,到达点C停止,设P运动了ts。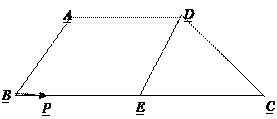

 于E,
于E, ,交AG于F.
,交AG于F. .
.