题目内容
已知一次函数的图象过点(0,3)和(-2,0),那么直线必过下面的点
- A.(4,6)
- B.(-4,-3)
- C.(6,9)
- D.(-6,6)
B
分析:根据“两点法”确定一次函数解析式,再检验直线解析式是否满足各点的横纵坐标.
解答:设经过两点(0,3)和(-2,0)的直线解析式为y=kx+b,
则 ,解得
,解得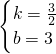 ,∴y=
,∴y= x+3;
x+3;
A、当x=4时,y= ×4+3=9≠6,点不在直线上;
×4+3=9≠6,点不在直线上;
B、当x=-4时,y= ×(-4)+3=-3,点在直线上;
×(-4)+3=-3,点在直线上;
C、当x=6时,y= ×6+3=12≠9,点不在直线上;
×6+3=12≠9,点不在直线上;
D、当x=-6时,y= ×(-6)+3=-6≠6,点不在直线上;
×(-6)+3=-6≠6,点不在直线上;
故选B.
点评:本题考查用待定系数法求直线解析式以及一定经过某点的函数应适合这个点的横纵坐标.
分析:根据“两点法”确定一次函数解析式,再检验直线解析式是否满足各点的横纵坐标.
解答:设经过两点(0,3)和(-2,0)的直线解析式为y=kx+b,
则
 ,解得
,解得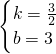 ,∴y=
,∴y= x+3;
x+3;A、当x=4时,y=
 ×4+3=9≠6,点不在直线上;
×4+3=9≠6,点不在直线上;B、当x=-4时,y=
 ×(-4)+3=-3,点在直线上;
×(-4)+3=-3,点在直线上;C、当x=6时,y=
 ×6+3=12≠9,点不在直线上;
×6+3=12≠9,点不在直线上;D、当x=-6时,y=
 ×(-6)+3=-6≠6,点不在直线上;
×(-6)+3=-6≠6,点不在直线上;故选B.
点评:本题考查用待定系数法求直线解析式以及一定经过某点的函数应适合这个点的横纵坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目