Question

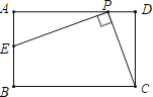
【题目】 如图，在矩形ABCD中，AB=6，BC=10，P是AD边上一动点(不含端点A，D)，连接PC，E是AB边上一点，设BE=a，若存在唯一点P，使∠EPC=90°，则a的值是(　　)

A.B.C.3D.6

Answer 1

【答案】B

【解析】

设AP=x，AE=y，证明△APE∽△DCP，根据相似三角形的性质得到比例式，转化为一元二次方程，利用判别式△=0，构建方程解决问题．

解：∵PE⊥PC，

∴∠APE+∠DPC=90°，

∵∠D=90°，

∴∠DCP+∠DPC=90°，

∴∠APE=∠DCP，又∠A=∠D=90°，

∴△APE∽△DCP，

∴=，

设AP=x，AE=y，

可得x(10-x)=6y，

∴x2-10x+6y=0，

由题意△=0，

∴100-24y=0，

∴y=，

∵BE=AB-AE=6-=，

故选：B．