题目内容
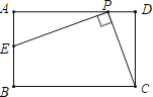
【题目】如图,△ABC内接于⊙O.AB为⊙O的直径,BC=3,AB=5,D、E分别是边AB、BC上的两个动点(不与端点A、B、C重合),将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上(包含端点A、C),若△ADB′为等腰三角形,则AD的长为___.

【答案】![]() 或
或![]() 或
或![]() .
.
【解析】
根据圆周角定理得到∠C=90°,根据勾股定理得到AC=4,根据折叠的性质得到BD=B′D,BE=B′E,①当AB′=DB′时,设AB′=DB′=BD=x,根据相似三角形的性质得到AD=5-x=![]() ;;②当AD=DB′时,则AD=DB′=BD=
;;②当AD=DB′时,则AD=DB′=BD=![]() AB=
AB=![]() ;③当AD=AB′时,如图2,过D作DH⊥AC于H,根据平行线分线段成比例定理即可得到结论.
;③当AD=AB′时,如图2,过D作DH⊥AC于H,根据平行线分线段成比例定理即可得到结论.
∵AB为⊙O的直径,

∴∠C=90°,
∵BC=3,AB=5,
∴AC=4,
∵将△BDE沿DE折叠,点B的对应点B′恰好落在线段AC上,
∴BD=B′D,BE=B′E,
若△ADB′为等腰三角形,
①当AB′=DB′时,设AB′=DB′=BD=x,
则AD=5-x,
如图1,过B′作B′F⊥AD于F,
则AF=DF=![]() AD,
AD,
∵∠A=∠A,∠AFB′=∠C=90°,
∴△AFB′∽△ACB,
∴![]() =
=![]() ,
,
∴![]() =
= ,
,
解得:x=![]() ,
,
∴AD=5-x=![]() ;
;
②当AD=DB′时,则AD=DB′=BD=![]() AB=
AB=![]() ;
;
③当AD=AB′时,如图2,过D作DH⊥AC于H,

∴DH∥BC,
∴![]() =
=![]() =
=![]() ,
,
设AD=5m,
∴DH=3m,AH=4m,
∴DB′=BD=5-5m,HB′=5m-4m=m,
∵![]() =
=![]() +
+![]() ,
,
∴![]() =
=![]() +
+![]() ,
,
∴m=![]() ,m=
,m=![]() (不合题意舍去),
(不合题意舍去),
∴AD=![]() ,
,
故答案为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
相关题目