题目内容
【题目】已知抛物线l1:y=![]() x2+c,当其函数值y=1时,只有一个自变量x的值与其对应
x2+c,当其函数值y=1时,只有一个自变量x的值与其对应
(1)求c的值;
(2)将抛物线l1经过平移得到抛物线l2:y=![]() (x﹣p)2﹣1.
(x﹣p)2﹣1.
①若抛物线l2与x轴交于A,B两点(A在B的左侧),与y轴交于点C,记△ABC的外心为P,当﹣1≤p≤![]() 时,求点P的纵坐标的取值范围;
时,求点P的纵坐标的取值范围;
②当0≤x≤2时,对于抛物线l1上任意点E,抛物线l2上总存在点F,使得点E、F纵坐标相等,求p的取值范围
【答案】(1)c=1;(2)①![]() ;②
;②![]() 和
和![]()
【解析】
![]() 只有一个x与其对应的函数值即顶点的值,进而求出c.
只有一个x与其对应的函数值即顶点的值,进而求出c.![]() ①用p表示A、B、C的坐标,由于外心是三角形三边垂直平分线的交点,故点P在抛物线
①用p表示A、B、C的坐标,由于外心是三角形三边垂直平分线的交点,故点P在抛物线![]() 的对称轴上,用p表示BC中点D,即直线PD垂直平分
的对称轴上,用p表示BC中点D,即直线PD垂直平分![]() 求出直线BC解析式的
求出直线BC解析式的![]() ,利用两直线垂直时,
,利用两直线垂直时,![]() ,求出直线PD解析式的
,求出直线PD解析式的![]() 并求出解析式,把
并求出解析式,把![]() 代入即用p表示出P的纵坐标.再由
代入即用p表示出P的纵坐标.再由![]() 计算点P纵坐标的范围.
计算点P纵坐标的范围.
②先求出![]() 时,对于抛物线
时,对于抛物线![]() 对应的函数值范围
对应的函数值范围![]() 根据题意,即
根据题意,即![]() 的每一个函数值,都能在抛物线
的每一个函数值,都能在抛物线![]() 上有对应的函数值,故抛物线
上有对应的函数值,故抛物线![]() 的函数值范围应比抛物线
的函数值范围应比抛物线![]() 的大,即最小值小于等于1,最大值大于等于
的大,即最小值小于等于1,最大值大于等于![]() 对抛物线
对抛物线![]() 的对称轴进行分类讨论,不同情况下在
的对称轴进行分类讨论,不同情况下在![]() 时的最大值最小值取值不相同,每种情况里根据“最小值小于等于1,最大值大于等于2”列出不等式
时的最大值最小值取值不相同,每种情况里根据“最小值小于等于1,最大值大于等于2”列出不等式![]() 组
组![]() ,即求出p的范围.
,即求出p的范围.
解:![]() 当
当![]() 函数值
函数值![]() 时,只有一个自变量x的值与其对应,
时,只有一个自变量x的值与其对应,![]() 抛物线的顶点纵坐标为1,
抛物线的顶点纵坐标为1,![]() .
.![]() ①当
①当![]() 时,解得:
时,解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,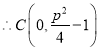 ,
,![]() 中点为
中点为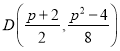 ,
,
设直线BC解析式为:![]() ,
,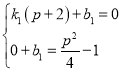 解得:
解得: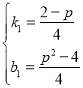 ,
,![]() 点P为
点P为![]() 的外心,
的外心,![]() 点P在抛物线
点P在抛物线![]() 对称轴上,直线PD垂直平分BC,
对称轴上,直线PD垂直平分BC,
设直线PD解析式为:![]() ,
,![]() ,即
,即![]() ,
,把D代入得:
![]() ,
,
解得:![]() ,
,![]() 直线PD解析式为:
直线PD解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,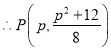 ,
,![]() ,
,![]() ,
,![]() 点P的纵坐标
点P的纵坐标![]() 的取值范围是
的取值范围是![]() ;
;
②对于抛物线![]() :
:![]() ,当
,当![]() 时,
时,![]() ,
,![]() 抛物线
抛物线![]() 上总存在点F,使得F纵坐标与
上总存在点F,使得F纵坐标与![]() 上任意点E的纵坐标相等,
上任意点E的纵坐标相等,![]() 抛物线
抛物线![]() 在
在![]() 时,y的取值范围比
时,y的取值范围比![]() 的大,即最小值值
的大,即最小值值![]() ,最大值
,最大值![]() ,
,![]() 若
若![]() ,则抛物线
,则抛物线![]() 在
在![]() 时,y随x的增大而增大,
时,y随x的增大而增大,![]() 时,最小值
时,最小值![]() ;
;![]() 时,最大值
时,最大值![]() ,
,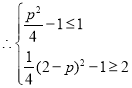 ,解得:
,解得:![]() ;
;![]() 若
若![]() ,则
,则![]() 时y最小,
时y最小,![]() 时y最大,
时y最大,![]() ,
,
解得:![]() 或
或![]() ,不成立;
,不成立;![]() 若
若![]() ,则
,则![]() 时y最小,
时y最小,![]() 时y最大,
时y最大,![]() ,
,
解得:![]() 或
或![]() ,不成立;
,不成立;![]() 若
若![]() ,则抛物线
,则抛物线![]() 在
在![]() 时,y随x的增大而减小,
时,y随x的增大而减小,![]() 时y最大,
时y最大,![]() 时y最小,
时y最小,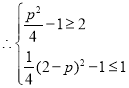 ,解得:
,解得:![]() ;
;
综上所述,p的取值范围为:![]() 和
和![]() .
.