题目内容
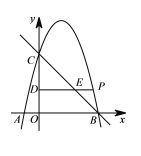
【题目】如图,四边形![]() 是矩形
是矩形
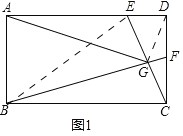
(1)如图1,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,
上的点,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
①求证:![]() ;
;
②若![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
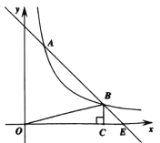
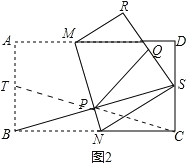
(2)如图2,将矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,点
处,点![]() 落在
落在![]() 边的点
边的点![]() 处,连接
处,连接![]() 交
交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点.若
的中点.若![]() ,
,![]() ,直接写出
,直接写出![]() 的最小值为 .
的最小值为 .

【答案】(1) ①见解析;②见解析;(2) ![]()
【解析】
(1)①证明△FBC∽△ECD可得结论.
②想办法证明∠AEB=∠AGB,可得sin∠AGB=sin∠AEB=![]() .
.
(2)如图2中,取AB的中点T,连接PT,CP.因为四边形MNSR与四边形MNBA关于MN对称,T是AB中点,Q是SR中点,所以PT=PQ,MN垂直平分线段BS,推出BP=PS,由∠BCS=90°,推出PC=PS=PB,推出PQ+PS=PT+PC,当T,P,C共线时,PQ+PS的值最小.
(1)①证明:如图1中,
∵四边形ABCD是矩形,
∴∠CDE=∥BCF=90°,
∵BF⊥CE,
∴∠BGC=90°,
∴∠BCG+∠FBC=∠BCG+∠ECD=90°,
∴∠FBC=∠ECD,
∴△FBC∽△ECD,
∴![]() .
.
②证明:如图1中,连接BE,GD.
∵BF⊥CE,EG=CG,
∴BF垂直平分线段EC,
∴BE=CB,∠EBG=∠CBG,
∵DG=CG,
∴∠CDG=∠GCD,
∵∠ADG+∠CDG=90°,∠BCG+∠ECD=90°,
∴∠ADG=∠BCG,
∵AD=BC,
∴△ADG≌△BCG(SAS),
∴∠DAG=∠CBG,
∴∠DAG=∠EBG,
∴∠AEB=∠AGB,
∴sin∠AGB=sin∠AEB=![]()
(2)如图2中,取AB的中点T,连接PT,CP.
∵四边形MNSR与四边形MNBA关于MN对称,T是AB中点,Q是SR中点,
∴PT=PQ,MN垂直平分线段BS,
∴BP=PS,
∵∠BCS=90°,
∴PC=PS=PB,
∴PQ+PS=PT+PC,
当T,P,C共线时,PQ+PS的值最小,最小值=![]() ,
,
∴PQ+PS的最小值为![]() .
.

【题目】二次函数![]() 为常数,
为常数,![]() 中的
中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
x | -1 | 0 | 3 |
y | n | -3 | -3 |
当![]() 时,下列结论中一定正确的是________(填序号即可)
时,下列结论中一定正确的是________(填序号即可)
①![]() ;②当
;②当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大;③
值的增大而增大;③![]() ;④当
;④当![]() 时,关于
时,关于![]() 的一元二次方程
的一元二次方程![]() 的解是
的解是![]() ,
,![]() .
.
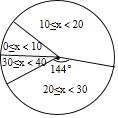
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.