Question

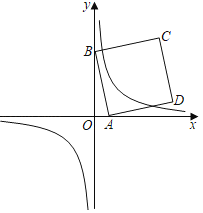
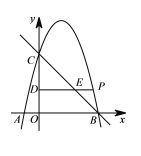
【题目】如图，在平面直角坐标系中，抛物线与轴交于点，点 的坐标分别是，与轴交于点．点在第一、二象限的抛物线上，过点作轴的平行线分别交轴和直线于点、．设点的横坐标为，线段的长度为．

⑴求这条抛物线对应的函数表达式；

⑵当点在第一象限的抛物线上时，求与之间的函数关系式；

⑶在⑵的条件下，当时，求的值．

Answer 1

【答案】（1）；（2）当时， ，当时， ；（3）或．

【解析】

（1）由题意直接根据待定系数法，进行分析计算即可得出函数解析式；

（2）根据自变量与函数值的对应关系，可得C点坐标，根据待定系数法，可得BC的解析式，根据E点的纵坐标，可得E点的横坐标，根据两点间的距离，可得答案；

（3）由题意根据PE与DE的关系，可得关于m的方程，根据解方程根据解方程，即可得出答案.

解：（1）由题意得，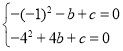

解得

∴这条抛物线对应的函数表达式是．

（2）当时，．

∴点的坐标是．

设直线的函数关系式为．

由题意得

解得

∴直线的函数关系式为．

∵PD∥x轴，

∴．

∴．

当时，如图①，．

当时，如图②，．

（3）当时，，．

∵，

∴．

解得（不合题意，舍去），．

当时，，．

∵，

∴．

解得（不合题意，舍去），．

综上所述，当时，或．