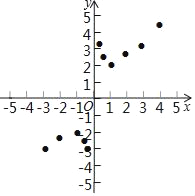题目内容
【题目】如图,已知正方形ABCD中,AB=4,点E,F在对角线BD上,AE∥CF.
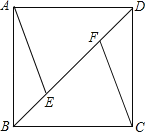
(1)求证:△ABE≌△CDF;
(2)若∠ABE=2∠BAE,求DF的长.
【答案】(1)见解析;(2)DF=4![]() ﹣4.
﹣4.
【解析】
(1)利用平行线性质和正方形的性质可得∠AEB=∠CFD,∠ABE=∠CDF,AB=CD,则借助AAS可证明△ABE≌△CDF;
(2)过点E作HE⊥BE,交AB于H点,证明∠HAE=∠HEA,得到AH=HE.设BE=DF=HE=AH=x,则HB=![]() x.根据AB=4,构造关于x的方程,解方程即可.
x.根据AB=4,构造关于x的方程,解方程即可.
解:(1)∵AE∥CF,
∴∠AEF=∠CFB.
∴∠AEB=∠CFD.
∵四边形ABCD是正方形,
∴∠ABE=∠CDF,AB=CD,
∴△ABE≌△CDF(AAS).
(2)过点E作HE⊥BE,交AB于H点,
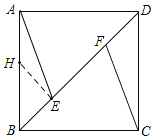
∴∠BHE=∠HBE=45°.
∵∠ABE=2∠BAE,
∴∠BHE=2∠BAE.
又∵∠BHE=∠HAE+∠AEH,
∴∠HAE=∠HEA.
∴AH=HE.
设BE=DF=HE=AH=x,
则HB=![]()
∴![]() =4,解得x=4
=4,解得x=4![]() ﹣4.
﹣4.
∴DF=4![]() ﹣4.
﹣4.

 阅读快车系列答案
阅读快车系列答案【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x=_____.
时,x=_____.
②写出该函数的一条性质_____.
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.