��Ŀ����
����Ŀ��С������ѧϰ�����ľ��飬�Ժ���y=x+![]() ��ͼ�������ʽ�����̽����
��ͼ�������ʽ�����̽����
������С����̽�����̣��벹��������
��1������y=x+![]() ���Ա���x��ȡֵ��Χ��_____��
���Ա���x��ȡֵ��Χ��_____��
��2���±��г���y��x�ļ����Ӧֵ����д��m��n��ֵ��m=_____��n=_____��
x | �� | ��3 | ��2 | ��1 | �� | �� |
|
| 1 | 2 | 3 | 4 | �� |
y | �� | �� | �� | ��2 | �� | �� | m |
| 2 |
| n |
| �� |
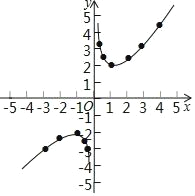
��3����ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣬��������ĵ㣬�����ú�����ͼ����
��4����Ϻ�����ͼ������ɣ�
�ٵ�y=��![]() ʱ��x=_____��
ʱ��x=_____��
��д���ú�����һ������_____��
��������x+![]() =t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
=t����������ȵ�ʵ��������t��ȡֵ��Χ��_____��
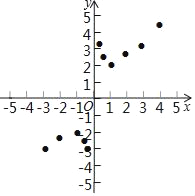
���𰸡���1��x��0����2��![]() ��
��![]() ����3������������4������4��
����3������������4������4��![]() ���ں���ͼ���ڵ�һ���������ҹ���ԭ��Գ�����t����2��t��2��
���ں���ͼ���ڵ�һ���������ҹ���ԭ��Գ�����t����2��t��2��
��������
��1���ɷ�ĸ��Ϊ0���ɵ��Ա���x��ȡֵ��Χ��x��0.
��2������ͼ����֪��m��n�ֱ�Ϊ��![]() ��x=3ʱ�ĺ���ֵ���������ʽ��
��x=3ʱ�ĺ���ֵ���������ʽ��![]() ����.
����.
��3����������ĵ�����ƽ����������.
��4���ٹ۲캯��ͼ���(2)�еı����У���![]() ʱ��x=4��
ʱ��x=4��![]() �ɵã���
�ɵã���![]() ʱ��x=-4��
ʱ��x=-4��![]() .
.
�ڹ۲캯����ͼ��д��������һ�����ʼ��ɣ������ԡ��Գ��ԡ�ͼ���������ȣ�.
�۴˷��̵ĸ��ɿ���![]() ��y=t�Ľ��㣬�ʷ�������������ȵ�ʵ�����ɿ���������������ͼ�����������㣬�۲�ͼ���֪����t>2��t<-2ʱ��������ͼ�����������㣬��t��ȡֵ��ΧΪ��t>2��t<-2.
��y=t�Ľ��㣬�ʷ�������������ȵ�ʵ�����ɿ���������������ͼ�����������㣬�۲�ͼ���֪����t>2��t<-2ʱ��������ͼ�����������㣬��t��ȡֵ��ΧΪ��t>2��t<-2.
�⣺��1����x�ڷ�ĸ�ϣ�
��x��0��
�ʴ�Ϊ��x��0��
��2����x=![]() ʱ��y=x+
ʱ��y=x+![]() =
=![]() ��
��
��x=3ʱ��y=x+![]() =
=![]() ��
��
�ʴ�Ϊ��![]() ��
��![]() ��
��
��3��������ߣ���������ͼ����
��4���ٵ�y=��![]() ʱ����x+
ʱ����x+![]() =��
=��![]() ��
��
��ã�x1=��4��x2=��![]() ��
��
�ʴ�Ϊ����4��![]() ��
��
�ڹ۲캯��ͼ��֪������ͼ���ڵ�һ���������ҹ���ԭ��Գƣ�
�ʴ�Ϊ������ͼ���ڵ�һ���������ҹ���ԭ��Գƣ�
�ۡ�x+![]() =t����������ȵ�ʵ������
=t����������ȵ�ʵ������
��t����2��t��2��
�ʴ�Ϊ��t����2��t��2��