题目内容
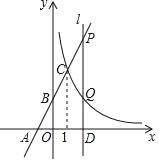
【题目】如图,平面直角坐标系中,矩形OABC的边与函数y=![]() (x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于( )
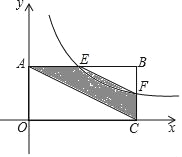
A. 4 B. 6 C. 8 D. 不能确定
【答案】B
【解析】
由四边形OABC是矩形,F是BC的中点,可设F(m,n),则B(m,2n),又E点在抛物线上,则E(![]() ,2n).可以用含m,n的式子表示出矩形OABC,三角形AOC和三角形BEF的面积.F在反比例函数的图形上可得到mn的关系,
,2n).可以用含m,n的式子表示出矩形OABC,三角形AOC和三角形BEF的面积.F在反比例函数的图形上可得到mn的关系,
再依据S四边形ACFE =S矩形OABC-S△AOC-S△BEF.即可求.
解:∵边形OABC是矩形,F是BC的中点,
∴可设F(m,n),则B(m,2n),又E点在抛物线上,则E(![]() ,2n),
,2n),
∵F在抛物线上,
∴mn=8,
∵F(m,n),B(m,2n), E(![]() ,2n),
,2n),
∴OA=2n,AB=OC=m,AE=![]() ,BF=n,
,BF=n,
∴S矩形OABC=2mn,
S△AOC =![]() ×OA×OC==
×OA×OC==![]() ×2n×m=mn,
×2n×m=mn,
S△BEF =![]() ×BE×BF=
×BE×BF=![]() ×(m-
×(m-![]() )×n=
)×n=![]() mn-4,
mn-4,
∵S四边形ACFE =S矩形OABC-S△AOC-S△BEF,
∴S四边形ACFE =2mn-mn-(![]() mn-4)=
mn-4)=![]() mn+2,
mn+2,
∵mn=8,
∴S四边形ACFE =![]() mn+2=6.
mn+2=6.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】垫球是排球队常规训练的重要项目之一,下列图表中的数据是运动员甲、乙、丙三人每人10次垫球测试的成绩,测试规则为每次连续接球10个,每垫球到位1个记1分,已知运动员甲测试成绩的中位数和众数都是7.
运动员甲测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 |
| 6 | 8 | 6 | 8 |
|
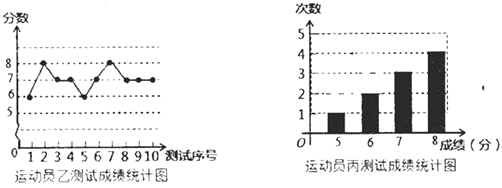
(1)填空:![]() ______;
______;![]() ______.
______.
(2)要从他们三人中选择一位垫球较为稳定的接球能手,你认为选谁更合适?为什么?