Question

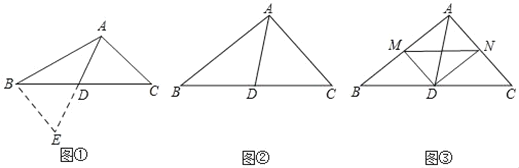
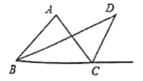
【题目】将一副三角尺按如图①方式拼接：含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合（在Rt△ABC中，∠ACB＝90°，∠BAC＝30°；在Rt△ACD中，∠ADC＝90°∠DAC＝45°）已知AB＝2，P是AC上的一个动点．

（1）当PD＝BC时，求∠PDA的度数；

（2）如图②，若E是CD的中点，求△DEP周长的最小值；

（3）如图③，当DP平分∠ADC时，在△ABC内存在一点Q，使得∠DQC＝∠DPC，且CQ＝，求PQ的长．

Answer 1

【答案】（1）∠PDA＝15°；（2）△PDE的周长的最小值为+；（3）PQ＝﹣．

【解析】

（1）作DM⊥AC交于M，由∠BAC=30°知BC：AC：AB=1：：2且AB=，从而得BC=，AC=3，再由AD：CD：AC=1：1：知AM=MC=DM=1.5；结合PD=BC=，求得PM=，从而知PM=PD，∠PDM=30°，继而得出答案；

（2）作△ADC关于直线AC对称，D的对称点为D′，知四边形AD′CD是正方形，连接D′E，PD，此时PD+PE=D′E，知△PDE的周长最小，得出CD=CD′=，CE=DE=，D′E=，从而得出答案；

（3）将△PQC绕点P逆时针旋转90°得到△PND，知△PNQ是等腰直角三角形，得∠PNQ=∠PQN=45°，据此知∠PQC=45°+90°=135°=∠PND，从而证D、N、Q三点共线得DN=CQ=，由勾股定理知QN=，根据PQ：PN：NQ=1：1：可得答案．

解：（1）如图1，过点D作DM⊥AC交于M，

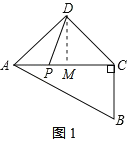
在Rt△ABC中，∠BAC＝30°，

∴BC：AC：AB＝1：：2，且AB＝，

∴BC＝，AC＝3，

在Rt△ADC中，AD：CD：AC＝1：1：，

∴AM＝MC＝DM＝1.5；

在Rt△PDM中，PD＝BC＝，

∴PM＝，

∴PM＝PD，

∴∠PDM＝30°，

∴∠PDA＝45°﹣30°＝15°；

（2）如图2，作△ADC关于直线AC对称，D的对称点为D′，

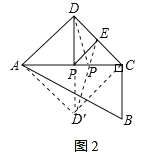
则四边形AD′CD是正方形，

连接D′E，PD，

此时PD+PE＝D′E，

∴△PDE的周长最小，

易得CD＝CD′＝，CE＝DE＝，

则D′E＝，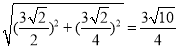

∴△PDE的周长的最小值为；

（3）如图3，将△PQC绕点P逆时针旋转90°得到△PND，

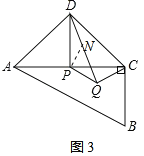
∵PN＝PQ，

∴△PNQ是等腰直角三角形，

∴∠PNQ＝∠PQN＝45°，

∴∠PQC＝45°+90°＝135°＝∠PND，

∴∠PND+∠PNQ＝135°+45°＝180°，

∴D、N、Q三点共线，

∴DN＝CQ＝，

在Rt△DQC中，DQ＝，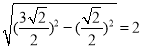

∴QN＝2﹣，

在等腰直角三角形NPQ中，PQ：PN：NQ＝1：1：，

∴PQ＝.