题目内容
如图,在菱形ABCD中,∠BAD=60°,点M是菱形对角线DB延长线上的一点,把△AMB绕点A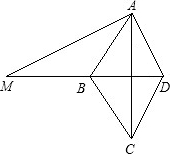 按逆时针方向旋转n度后恰好与△ACD重合.
按逆时针方向旋转n度后恰好与△ACD重合.(1)请直接写出n的值;
(2)若AD=1,试求点M在上述旋转过程中所经过的路线的长.
分析:(1)∵把△AMB绕点A按逆时针方向旋转与△ACD重合,可知旋转中心为点A,AB,AC为对应边,∠BAD就是旋转角,即n=60;
(2)点M的旋转路径是以A为圆心,AM为半径,60°的圆弧,AM=AC,计算菱形的对角线AC的长,用弧长公式求解.
(2)点M的旋转路径是以A为圆心,AM为半径,60°的圆弧,AM=AC,计算菱形的对角线AC的长,用弧长公式求解.
解答: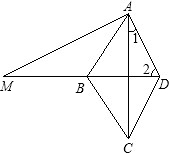 解:(1)∵把△AMB绕点A按逆时针方向旋转与△ACD重合,
解:(1)∵把△AMB绕点A按逆时针方向旋转与△ACD重合,
可知旋转中心为点A,
AB,AC为对应边,∠BAD就是旋转角,
即n=60;
(2)∵四边形ABCD是菱形
∴AC平分∠BAD,AC⊥BD
∴∠1=
×60°=30°,∠2=90°-∠1=60°
由(1)得:∠MAC=60°
∴∠MAD=90°
在Rt△AMD中,AD=1,tan∠2=
即tan60°=
∴AM=
∴l弧MC=
=
.
即点M在旋转过程中所经过的路线的长为
.
 解:(1)∵把△AMB绕点A按逆时针方向旋转与△ACD重合,
解:(1)∵把△AMB绕点A按逆时针方向旋转与△ACD重合,可知旋转中心为点A,
AB,AC为对应边,∠BAD就是旋转角,
即n=60;
(2)∵四边形ABCD是菱形
∴AC平分∠BAD,AC⊥BD
∴∠1=
| 1 |
| 2 |
由(1)得:∠MAC=60°
∴∠MAD=90°
在Rt△AMD中,AD=1,tan∠2=
| AM |
| AD |
即tan60°=
| AM |
| 1 |
∴AM=
| 3 |
∴l弧MC=
60•π•
| ||
| 180 |
| ||
| 3 |
即点M在旋转过程中所经过的路线的长为
| ||
| 3 |
点评:本题考查了找旋转图形的对应边,旋转角的方法,应明确点绕旋转中心所走路径是圆弧.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
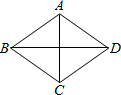 如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )
如图:在菱形ABCD中,AC=6,BD=8,则菱形的边长为( )| A、5 | B、10 | C、6 | D、8 |
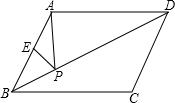
 ME交射线CD于点N,连接MD、AN.
ME交射线CD于点N,连接MD、AN. (2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA=
(2013•攀枝花)如图,在菱形ABCD中,DE⊥AB于点E,cosA= 如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.
如图,在菱形ABCD中,AE⊥BC,垂足为F,EC=1,∠B=30°,求菱形ABCD的周长.