题目内容
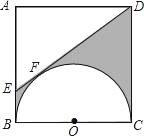
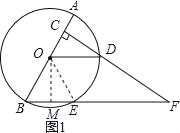
【题目】如图,已知AB是⊙O的直径,且AB=4,点C在半径OA上(点C与点O、点A不重合),过点C作AB的垂线交⊙O于点D.连接OD,过点B作OD的平行线交⊙O于点E,交CD的延长线于点F.
(1)若点E是![]() 的中点,求∠F的度数;
的中点,求∠F的度数;
(2)求证:BE=2OC;
(3)设AC=x,则当x为何值时BEEF的值最大?最大值是多少?

【答案】(1)∠F=30°;(2)见解析;(3)当x=![]() 时,最大值=9.
时,最大值=9.
【解析】分析:
(1)如图,连接OE,由OD∥OE可得∠DOE=∠OEB,由点E是![]() 的中点可得∠DOE=∠BOE,由OB=OE可得∠OBE=∠OEB,由此可得∠OBE=∠OEB=∠BOE=60°,结合CF⊥AB即可得到∠F=30°;
的中点可得∠DOE=∠BOE,由OB=OE可得∠OBE=∠OEB,由此可得∠OBE=∠OEB=∠BOE=60°,结合CF⊥AB即可得到∠F=30°;
(2)过点O作OM⊥BE于点M,由此可得BE=2BM,再证△OBM≌△DOC可得BM=OC,这样即可得到结论BE=2OC;
(3)由OD∥BF可得△COD∽△CBF,由此可得![]() ,由AB=4,AC=x结合(2)中结论可得OD=OB=BE=2,BC=4-x,OC=2-x,BE=2OC=4-2x,由此即可解得BF=
,由AB=4,AC=x结合(2)中结论可得OD=OB=BE=2,BC=4-x,OC=2-x,BE=2OC=4-2x,由此即可解得BF=![]() ,从而可得EF=BF-BE=
,从而可得EF=BF-BE=![]() ,这样即可把BEEF用含x的代数式表达出来,化简配方即可求得所求答案了.
,这样即可把BEEF用含x的代数式表达出来,化简配方即可求得所求答案了.
详解:
(1)如图1,连接OE.
∵![]() ,
,
∴∠BOE=∠EOD,
∵OD∥BF,
∴∠DOE=∠BEO,
∵OB=OE,
∴∠OBE=∠OEB,
∴∠OBE=∠OEB=∠BOE=60°,
∵CF⊥AB,
∴∠FCB=90°,
∴∠F=30°;
(2)如图1,过O作OM⊥BE于M,
∵OB=OE,
∴BE=2BM,
∵OD∥BF,
∴∠COD=∠B,
在△OBM与△DOC中 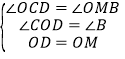 ,
,
∴△OBM≌△DOC,
∴BM=OC,
∴BE=2OC;
(3)∵OD∥BF,
∴△COD∽△CBF,
∴![]() ,
,
∵AC=x,AB=4,
∴OA=OB=OD=2,
∴OC=2﹣x,BE=2OC=4﹣2x,
∴![]() ,
,
∴BF=![]() ,
,
∴EF=BF﹣BE=![]() ,
,
∴BEEF=![]() ,
,
∴当![]() 时,最大值=9.
时,最大值=9.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案