题目内容
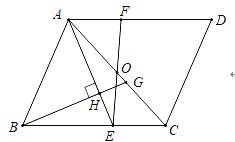
【题目】如图,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点F.过点
于点F.过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若![]() .
.
①求证:![]() ;
;
②探索![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
【答案】(1)见解析;(2)①见解析,②![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据平行四边形的性质得到∠OAF=∠OCE,证明△OAF≌△OCE,根据全等三角形的对应边相等证明结论;
(2)①过A作AM⊥BC于M,交BG于K,过G作GN⊥BC于N,根据三角形的外角性质得到∠BAG=∠BGA;
②证明△AME≌△BNG,根据全等三角形的性质得到ME=NG,根据等腰直角三角形的性质得到BE=![]() GC,根据(1)中结论证明即可.
GC,根据(1)中结论证明即可.
(1)证明:∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
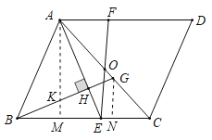
(2)①过![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,又
,又![]() ,
,
∴![]() ,
,
设![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ;
;
②![]() ,
,
理由如下:∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
在等腰![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目