题目内容
如图,已知弦AB与半径相等,连结OB,并延长使BC=OB.
小题1:问AC与⊙O有什么关系.
小题2:请你在⊙O上找出一点D,使AD=AC(自己完成作图,并证明你的结论).
小题1:问AC与⊙O有什么关系.
小题2:请你在⊙O上找出一点D,使AD=AC(自己完成作图,并证明你的结论).
小题1:AC与⊙O相切.
小题2:略
解:(1)证明:如图,
∵AB与半径相等,∴∠OAB=60°,∠OBA=60°.
∵BC=OB=AB,∴∠BAC=30°,
∴∠OAC=90°,∴AC与⊙O相切.
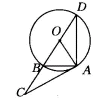
(2)①延长BO交⊙O于D,则必有AD=AC.
证明:∵∠BOA=60°,OA=OD,
∴∠D=30°.又∵∠C=30°,
∴∠C=∠D,∴AD=AC.
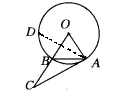
②作∠OAB的角平分线交⊙O于D,则AD=AC
证明略
∵AB与半径相等,∴∠OAB=60°,∠OBA=60°.
∵BC=OB=AB,∴∠BAC=30°,
∴∠OAC=90°,∴AC与⊙O相切.

(2)①延长BO交⊙O于D,则必有AD=AC.
证明:∵∠BOA=60°,OA=OD,
∴∠D=30°.又∵∠C=30°,
∴∠C=∠D,∴AD=AC.
②作∠OAB的角平分线交⊙O于D,则AD=AC
证明略


练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
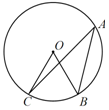
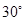 ,则∠A的度数为 ▲ .
,则∠A的度数为 ▲ .
 是正方形
是正方形 的外接圆,点
的外接圆,点 是
是 上任意一点,则∠
上任意一点,则∠ 的度数为( ▲ )
的度数为( ▲ )
 ,
, .
.
 cm,则此扇形的面积为___________.
cm,则此扇形的面积为___________.