��Ŀ����
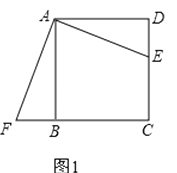
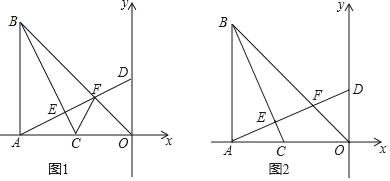
����Ŀ����ͼ����Rt��ABO�У���BAO��90����AO��AB��BO��8![]() ����A�����꣨��8��0������C���߶�AO����ÿ��2����λ���ȵ��ٶ���A��O�˶����˶�ʱ��Ϊt�룬����BC������A��AD��BC������Ϊ��E���ֱ�BO�ڵ�F����y���ڵ� D��
����A�����꣨��8��0������C���߶�AO����ÿ��2����λ���ȵ��ٶ���A��O�˶����˶�ʱ��Ϊt�룬����BC������A��AD��BC������Ϊ��E���ֱ�BO�ڵ�F����y���ڵ� D��
��1����t��ʾ��D�������� ����
��2����ͼ1������CF����t��2ʱ����֤����FCO����BCA��
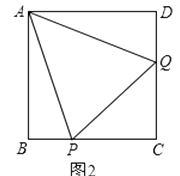
��3����ͼ2����BCƽ�֡�ABOʱ����t��ֵ��
���𰸡���1����0��2t������2������������3��t=4��![]() ��1��
��1��
��������
��1������֪������֤����ABC�ա�OAD������ȫ�������ε����ʼ��������D�����ꣻ
��2���ɣ�1���Ľ��ۿ�֤����FOD�ա�FOC���Ӷ���FCO����FDO���ٸ��ݣ�1���С�ABC�ա�OAD���ɵá�ACB����ADO��������FCO����ACB��֤��
��3����AB��ȡһ��K��ʹ��AK��AC������CK����AK��AC��m����CK��![]() m�����ݽ�ƽ���ߵ����ʺ���������ǺͶ����ɵ�KB��KC��
m�����ݽ�ƽ���ߵ����ʺ���������ǺͶ����ɵ�KB��KC��![]() m���Ӷ����m��ֵ������t��ֵҲ�����.
m���Ӷ����m��ֵ������t��ֵҲ�����.
�⣺��1����AD��BC��
���AEB��90������BAC����AOD��
���ABC+��BAE��90������BAE+��OAD��90����
���ABC����OAD��
��AB��OA��
���ABC�ա�OAD��ASA����
��OD��AC��2t��
��D��0��2t����
�ʴ�Ϊ��0��2t����
��2����ͼ1�У�
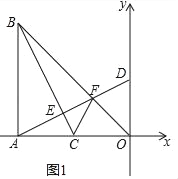
��AB��AO����BAO��90����OB��![]() ��
��
��AB��AO��8��
��t��2��
��AC��OD��4��
��OC��OD��4��
��OF��OF����FOD����FOC��
���FOD�ա�FOC��SAS����
���FCO����FDO��
�ߡ�ABC�ա�OAD��
���ACB����ADO��
���FCO����ACB��
��3����ͼ2�У���AB��ȡһ��K��ʹ��AK��AC������CK����AK��AC��m����CK��![]() m��
m��
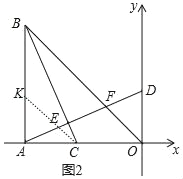
��CBƽ�֡�ABO��
���ABC��22.5����
�ߡ�AKC��45������ABC+��KCB��
���KBC����KCB��22.5����
��KB��KC��![]() m��
m��
��m+![]() m��8��
m��8��
��m��8��![]() ����
����
��t��![]() ��4��
��4��![]() ��1����
��1����

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�