Question

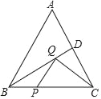
【题目】如图，△ABC是等腰直角三角形，AB＝BC，O是△ABC内部的一个动点，△OBD是等腰直角三角形，OB＝BD．

（1）求证：∠AOB＝∠CDB；

（2）若△COD是等腰三角形，∠AOC＝140°，求∠AOB的度数．

Answer 1

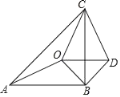
【答案】（1）详见解析；（2）∠AOB的度数为110°或95°或125°．

【解析】

（1）根据等腰直角三角形的性质和全等三角形的判定和性质解答即可；

（2）设∠AOB的度数为x，分三种情况进行解答即可．

（1）∵△ABC和△OBD是等腰直角三角形，

∴AB＝BC，OB＝BD，∠ABC＝∠OBD＝90°，

∵∠ABO+∠OBC＝∠CBD+∠OBC，

∴∠ABO＝∠CBD，

在△ABO和△CBD中

，

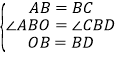∴△ABO≌△CBD（SAS），

∴∠AOB＝∠CDB；

（2）设∠AOB的度数为x，则∠CDB＝x，∠CDO＝x﹣45°，

∠COD＝∠COB﹣∠DOB＝360°﹣140°﹣x﹣45°＝175°﹣x，

∠OCD＝180°﹣∠CDO﹣∠COD＝50°，

①当∠CDO＝∠COD时，x﹣45°＝175°﹣x，解得：x＝110°，

②当∠CDO＝∠OCD时，x﹣45°＝50°，解得：x＝95°，

③当∠COD＝∠OCD时，175°﹣x＝50°，解得：x＝125°，

故∠AOB的度数为110°或95°或125°．