题目内容
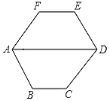
【题目】如图,六边形ABCDEF的内角都相等,∠FAD=60°.
(1)求∠ADE的度数;
(2)求证:EF∥BC.
【答案】(1)∠ADE=60°;(2)详见解析.
【解析】
(1)由于六边形的内角和为720°,然后利用六边形ABCDEF的内角都相等得到每个内角的度数为120°,而∠DAB=60°,四边形ABCD的内角和为360°,由此即可分别求出∠CDA和∠EDA,最后利用平行线的判定方法即可推知AB∥DE,根据平行线的性质即可得到结论;
(2)根据平行线的判定即可得到结论.
(1)∵六边形ABCDEF的内角都相等,
∴∠BAF=∠B=∠C=∠CDE=∠E=∠F=120°,
∵∠FAD=60°,
∴∠F+∠FAD=180°,
∴EF∥AD,
∴∠E+∠ADE=180°,
∴∠ADE=60°;
(2)∵∠BAD=∠FAB﹣∠FAD=60°,
∴∠BAD+∠B=180°,
∴AD∥BC,
∴EF∥BC.

【题目】根据表中的信息判断,下列语句中正确的是( )
x | 15 | 15.1 | 15.2 | 15.3 | 15.4 | 15.5 | 15.6 | 15.7 | 15.8 | 15.9 | 16 |
x2 | 225 | 228.01 | 231.04 | 234.09 | 237.16 | 240.25 | 243.36 | 246.49 | 249.64 | 252.81 | 256 |
A.![]()
B.235的算术平方根比15.3小
C.只有3个正整数n满足15.5![]()
D.根据表中数据的变化趋势,可以推断出16.12将比256增大3.19
【题目】国家发改委、工业和信息化部、财政部公布了“节能产品惠民工程”,公交公司积极响应将旧车换成节能环保公交车,计划购买A型和B型两种环保型公交车10辆,其中每台的价格、年载客量如表:
A型 | B型 | |
价格(万元/台) | x | y |
年载客量/万人次 | 60 | 100 |
若购买A型环保公交车1辆,B型环保公交车2辆,共需400万元;若购买A型环保公交车2辆,B型环保公交车1辆,共需350万元.
(1)求x、y的值;
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保10辆公交车在该线路的年载客量总和不少于680万人次,问有哪几种购买方案?
(3)在(2)的条件下,哪种方案使得购车总费用最少?最少费用是多少万元?