题目内容
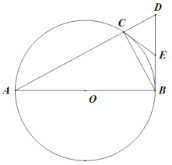
【题目】如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.给出下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心;④APAD=CQCB.其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②③④
【答案】B
【解析】
①错误,假设成立,推出矛盾即可;
②正确.想办法证明∠GPD=∠GDP即可;
③正确.想办法证明PC=PQ=PA即可;
④正确.证明△APF∽△ABD,可得APAD=AFAB,证明△ACF∽△ABC,可得AC2=AFAB,证明△CAQ∽△CBA,可得AC2=CQCB,由此即可解决问题;
解:①错误,假设∠BAD=∠ABC,则弧BD=弧AC,
∵弧AC=弧CD,
∴弧BD=弧AC=弧CD,显然不可能,故①错误.
②正确.连接OD.
∵GD是切线,
∴DG⊥OD,
∴∠GDP+∠ADO=90°,
∵OA=OD,
∴∠ADO=∠OAD,
∵∠APF+∠OAD=90°,∠GPD=∠APF,
∴∠GPD=∠GDP,
∴GD=GP,故②正确.
③正确.∵AB⊥CE,
∴弧AE=弧AC,
∵弧AC=弧CD,
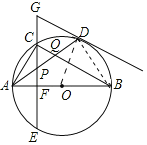
∴弧CD=弧AE,
∴∠CAD=∠ACE,
∴PC=PA,
∵AB是直径,
∴∠ACQ=90°,
∴∠ACP+∠QCP=90°,∠CAP+∠CQP=90°,
∴∠PCQ=∠PQC,
∴PC=PQ=PA,
∵∠ACQ=90°,
∴点P是△ACQ的外心.故③正确.
④正确.连接BD.
∵∠AFP=∠ADB=90°,∠PAF=∠BAD,
∴△APF∽△ABD,
∴![]() =
=![]() ,
,
∴APAD=AFAB,
∵∠CAF=∠BAC,∠AFC=∠ACB=90°,
∴△ACF∽△ABC,
可得AC2=AFAB,
∵∠ACQ=∠ACB,∠CAQ=∠ABC,
∴△CAQ∽△CBA,可得AC2=CQCB,
∴APAD=CQCB.故④正确,
故选:B.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案