题目内容
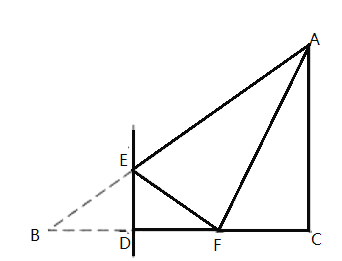
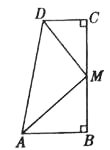
【题目】已知,如图,四边形![]() 中,
中,![]() ,
,![]() 是
是![]() 中点,
中点,![]() 平分
平分![]() .连接
.连接![]() .
.
(1)![]() 是否平分
是否平分![]() ?请证明你的结论;
?请证明你的结论;
(2)线段![]() 与
与![]() 有怎样的位置关系?请说明理由.
有怎样的位置关系?请说明理由.
【答案】(1)AM平分∠BAD,理由见详解;(2)AM⊥DM,理由见详解.
【解析】
(1)由题意过点M作ME⊥AD,垂足为E,先求出ME=MC,再求出ME=MB,从而证明AM平分∠BAD;
(2)根据题意利用两直线平行同旁内角互补可得∠1+∠3=90°,从而求证两直线垂直.
解:(1)AM平分∠BAD,理由为:
证明:过点M作ME⊥AD,垂足为E,
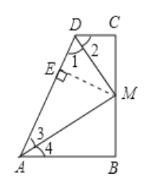
∵DM平分∠ADC,
∴∠1=∠2,
∵MC⊥CD,ME⊥AD,
∴ME=MC(角平分线上的点到角两边的距离相等),
又∵![]() 是
是![]() 中点,MC=MB,
中点,MC=MB,
∴ME=MB,
∵MB⊥AB,ME⊥AD,
∴AM平分∠BAD(到角的两边距离相等的点在这个角的平分线上).
(2)AM⊥DM,理由如下:
∵∠B=∠C=90°,
∴DC⊥CB,AB⊥CB,
∴CD∥AB(垂直于同一条直线的两条直线平行),
∴∠CDA+∠DAB=180°(两直线平行,同旁内角互补),
又∵∠1=![]() ∠CDA,∠3=
∠CDA,∠3=![]() ∠DAB(角平分线定义),
∠DAB(角平分线定义),
∴2∠1+2∠3=180°,
∴∠1+∠3=90°,
∴∠AMD=90°,即AM⊥DM.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目