题目内容
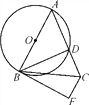
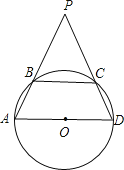
【题目】已知ABCD是一个以AD为直径的圆内接四边形,分别延长AB和DC,它们相交于P,若∠APD=60°,AB=5,PC=4,则⊙O的面积为( )
A. 25π B. 16π C. 15π D. 13π
【答案】D
【解析】
连接AC,由圆周角定理可得出∠ACD=90°,再由圆内接四边形的性质及三角形内角和定理可求出∠PAC=30°,由直角三角形的性质可求出AP、AC的长,由相似三角形的判定定理及性质可得出CD的长,再根据勾股定理接可求出AD的长,进而求出该圆的面积.
连接AC,
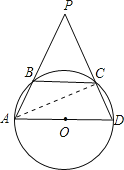
∵AD是⊙O的直径,
∴∠ACD=90°,
∵∠APD=60°,
∴∠PAC=30°,
∴AP=2PC=2×4=8,
∵AB=5,
∴PB=8-5=3,
∵四边形ABCD是以AD为直径的圆内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB,∠APD=∠APD,
∴△PCB∽△PAD,
∴![]() ,即
,即![]() ,PD=6,
,PD=6,
∴CD=PD-PC=6-4=2,
∴AC=![]() ,
,
在Rt△ACD中,AD=![]() .
.
∴OA=![]() AD=
AD=![]() ,
,
∴⊙O的面积=π×(![]() )2=13π.
)2=13π.
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目