Question

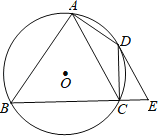
【题目】如图，已知内接于，为的直径，，交的延长线于点．

（1）为的中点，连结，求证：是的切线．

（2）若，求的大小．

Answer 1

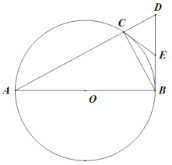
【答案】（1）证明见解析（2）30°

【解析】

（1）想要证明CE是⊙O的切线，证明∠OCE=90°即可，连接半径OC，根据同圆的半径相等和直角三角形斜边中线等于斜边一半可得：∠EBC+∠OBC=∠ECB+∠OCB，则∠OCE=∠OBE=90°，可得结论；

（2）设CD=m，则AC=3m，证明△ACB∽△BCD，列比例式可得：BC=m，利用三角函数定义可得结论．

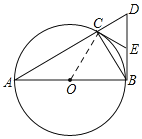
（1）连接OC，

∵为的直径，

∴∠ACB=∠DCB=90°，

∵为的中点，

∴BE=CE，

∴∠EBC=∠ECB，

∵OC=OB，

∴∠OCB=∠OBC，

∴∠ECB+∠OCB=∠EBC+∠OBC，

∵，

∴∠OCE=∠OBE=90°，

∴是的切线．

（2）设CD=m,则AC=3m，

∵△ACB≌△BCD，

∴，

∴，

∴，

∴，

∴=30°.