题目内容
【题目】如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a﹣4)2+![]() =0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
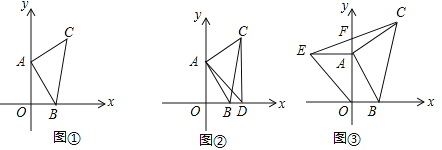
(1)求C点坐标;
(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;
(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值 (不需要解答过程或说明理由).
【答案】(1)C点坐标为(4,5);(2)∠ADC=45°;(3)2.
【解析】试题分析:(1)作CM⊥OA于M,由非负性质求出a=4,b=1,由AAS证明△CAM≌△ABO,得出MC=OA=4,MA=OB=1,求出OM=OA+MA=5,即可得出C点坐标;
(2)证出OD=OA,得出△OAD为等腰直角三角形,得出∠ADO=45°,求出∠ADC=45°即可;
(3)先判断出△AEF≌△MCF,进而求出AM,最后用三角形的面积公式即可得出结论;
试题解析:(1)作CM⊥OA于M,如图①所示:
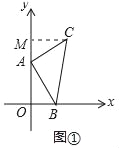
则∠CMA=∠AOB=90°,
∴∠OAB+∠ABO=90°,
∵(a﹣4)2+![]() =0,
=0,
∴a﹣4=0,b﹣1=0,
∴a=4,b=1,
∴OA=4,OB=1,
∵∠CAB=90°,
∴∠OAB+∠CAM=90°,
∴∠CAM=∠ABO,
在△CAM和△ABO中,
 ,
,
∴△CAM≌△ABO(AAS),
∴MC=OA=4,MA=OB=1,
∴OM=OA+MA=5,
∴C点坐标为(4,5);
(2)∵CD⊥x轴,∴D(4,0),
∴OD=OA,
∴△OAD为等腰直角三角形,
∴∠ADO=45°,
∴∠ADC=90°﹣45°=45°;
(3)A点在运动过程中S△AOB:S△AEF的值不会发生变化,S△AOB:S△AEF=2;
理由如下:作CM⊥OA于M,如图③所示:
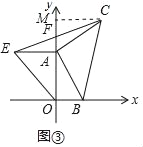
由(1)知,A(0,4),C(4,5),
∴OA=CM=4,
∵△AEO是等腰直角三角形,
∴AE=OA=4,∠OAE=90°,
∴∠EAF=∠OAE=90°=∠CMF,
∵∠AFE=∠MFC,AE=CM,
∴△AEF≌△MCF,
∴AF=MF=![]() AM,
AM,
∵C(4,5),A(0,4),
∴AM=1,
∴MF=![]() ,
,
∴S△AEF=S△MCF=![]() MF×CM=
MF×CM=![]() ×
×![]() ×4=1,
×4=1,
S△AOB=![]() OA×OB=
OA×OB=![]() ×4×1=2,
×4×1=2,
∴S△AOB:S△AEF=2:1=2,
即S△AOB:S△AEF的值是定值,不会发生变化.

【题目】某天,一蔬菜经营户用60元钱从蔬菜批发市场批了西红柿和豆角共40㎏到菜市场去卖,西红柿和豆角这天的批发价与零售价如下表所示:问:他当天卖完这些西红柿和豆角能赚多少钱?
品名 | 西红柿 | 豆角 |
批发价(单位:元/kg) | 1.2 | 1.6 |
零售价(单位:元/kg) | 1.8 | 2.5 |