Question

【题目】“五一”假期，黔西南州某公司组织部分员工分别到甲、乙、丙、丁四地考察，公司按定额购买了前往各地的车票，如图所示是用来制作完整的车票种类和相应数量的条形统计图，根据统计图回答下列问题：

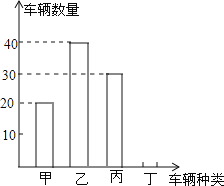
（1）若去丁地的车票占全部车票的10%，请求出去丁地的车票数量，并补全统计图（如图所示）．

（2）若公司采用随机抽取的方式发车票，小胡先从所有的车票中随机抽取一张（所有车票的形状、大小、质地完全相同、均匀），那么员工小胡抽到去甲地的车票的概率是多少？

（3）若有一张车票，小王和小李都想去，决定采取摸球的方式确定，具体规则：“每人从不透明袋子中摸出分别标有1、2、3、4的四个球中摸出一球（球除数字不同外完全相同），并放回让另一人摸，若小王摸得的数字比小李的小，车票给小王，否则给小李．”试用列表法或画树状图的方法分析这个规则对双方是否公平？

Answer 1

【答案】（1）丁地车票数为10张，补全条形统计图见解析；（2）；（3）不公平．

【解析】

（1）根据丁地车票的百分比求出甲，乙，丙地车票所占的百分比之和，用甲，乙，丙车票之和除以百分比求出总票数，得出丁车票的数量，补全条形统计图即可．

（2）根据甲，乙，丙，丁车票总数，与甲地车票数为20张，即可求出所求的概率．

（3）列表或画树状图得出所有等可能的情况数，求出两人获胜概率，比较即可得到公平与否．

解：（1）根据题意得：（20+40+30）÷（1﹣10%）=100（张），

则丁地车票数为100﹣（20+40+30）=10（张）．补全图形，如图所示：

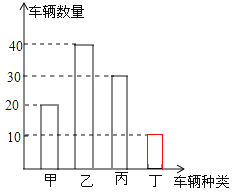
（2）∵总票数为100张，甲地票数为20张，

∴员工小胡抽到去甲地的车票的概率为．

（3）列表如下：

	1	2	3	4
1	（1，1）	（2，1）	（3，1）	（4，1）
2	（1，2）	（2，2）	（3，2）	（4，2）
3	（1，3）	（2，3）	（3，3）	（4，3）
4	（1，4）	（2，4）	（3，4）	（4，4）

∵所有等可能的情况数有16种，其中小王掷得数字比小李掷得的数字小的有6种：（1，2），（1，3），（1，4），（2，3），（2，4），（3，4），

P(小王掷得的数字比小李小)= ，P(小王掷得的数字不比小李小)=

∵P(小王掷得的数字比小李小)≠P(小王掷得的数字不比小李小)

∴这个规则不公平．