题目内容
【题目】2019年12月以来,湖北省武汉市部分医院陆续发现不明原因肺炎病例,现已证实该肺炎为一种新型冠状病毒感染的肺炎,其传染性较强.为了有效地避免交叉感染,需要采取以下防护措施:①戴口罩;②勤洗手;③少出门;④重隔离;⑤捂口鼻;⑥谨慎吃.某公司为了解员工对防护措施的了解程度(包括不了解、了解很少、基本了解和很了解),通过网上问卷调查的方式进行了随机抽样调查(每名员工必须且只能选择一项),并将调查结果绘制成如下两幅统计图.
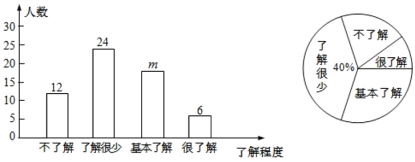
请你根据上面的信息,解答下列问题
(1)本次共调查了_______名员工,条形统计图中![]() ________;
________;
(2)若该公司共有员工1000名,请你估计不了解防护措施的人数;
(3)在调查中,发现有4名员工对防护措施很了解,其中有3名男员工、1名女员工.若准备从他们中随机抽取2名,让其在公司群内普及防护措施,求恰好抽中一男一女的概率.
【答案】(1)60 ,18;(2)估计不了解防护措施的人数为200名;(3)恰好抽中一男一女的概率为![]() .
.
【解析】
(1)用“了解很少”的人数除以它所占的比例即可得到调查的总人数,再用总人数减去“不了解”的人数、“了解很少”的人数及“很了解”的人数即可得到m;
(2)用1000乘以样本中“不了解”的人数所占的比例即可;
(3)列表展示出所有12种等可能的结果数,再找出恰好抽中一男一女的结果数,然后根据概率公式即可求解.
(1)由统计图可知,“了解很少”的员工有24名,其所占的百分比为40%,
故本次调查的员工人数为![]() (名),
(名),
∴![]() ,
,
故答案为:60 ,18;
(2)![]() (名).
(名).
答:估计不了解防护措施的人数为200名.
(3)根据题意,列表如下:
第1名 | 第2名 | |||
|
|
| 女 | |
|
|
|
| |
|
|
|
| |
|
|
|
| |
女 |
|
|
| |
由上表可知,共有12种结果,每种结果出现的可能性都相等,其中恰好抽中一男一女的结果有6种,
故所求概率为![]() .
.

 应用题作业本系列答案
应用题作业本系列答案【题目】某水果经销商上月份销售一种新上市的水果,平均售价为10元/千克,月销售量为1000千克.经市场调查,若将该种水果价格调低至x元/千克,则本月份销售量y(千克)与x(元/千克)之间符合一次函数关系,并且得到了表中的数据:
价格x(元/千克) | 7 | 5 |
价格y(千克) | 2000 | 4000 |
(1)求y与x之间的函数解析式;
(2)已知该种水果上月份的成本价为5元/千克,本月份的成本价为4元/千克,要使本月份销售该种水果所获利润比上月份增加20%,同时又要让顾客得到实惠,那么该种水果价格每千克应调低至多少元?