Question

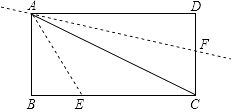
【题目】如图，在直角梯形ABCD中，AD∥BC，∠B＝90°，E为AB上一点，且ED平分∠ADC，EC平分∠BCD，则下列结论中错误的是（　　）

A. AE＝BE B. DE⊥CE C. CD＝AD+BC D. CD＝AD+CE

Answer 1

【答案】D

【解析】

根据直角梯形、等腰三角形的判定与性质以及全等三角形的判定与性质进行分析、 判断,可得正确的选择.

解:B,AD//BC,∠ADC+∠BCD=180,

ED平分∠ADC,EC平分∠BCD,

∠EDC=∠ADC, ∠DCE=∠DCB,

∠EDC+∠DCE= 180=90,

∠DEC=180-90=90,

故B选项不符合题意；

A、C选项,延长DE交CB的延长线于点F.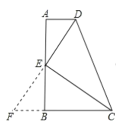

AD//BC, DE是∠ADC的角平分线,

∠CDF=∠ADE=∠DFC ,

CD=CF,

△CDF 是等腰三角形;

又由前面得DE⊥EC,

DE=FE,

又∠AED=∠BEF,

△BEF≌△AED,

AE=EB,

故A选项不符合题意；

AD=BF,又 CD=CF，

CD=CF=BC+BF=AD+BC,

故C选项不符合题意,

无法得出D选项，

故本题答案：D