题目内容
【题目】如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3 ![]() ,BC=3
,BC=3 ![]() ,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 .
,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为 . 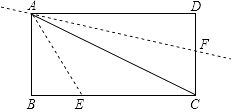
【答案】2 ![]()
【解析】解:∵四边形ABCD是矩形,
∴∠B=∠BAD=90°,
∵AB=3 ![]() ,BC=3
,BC=3 ![]() ,
,
∴tan∠BAC= ![]() =
= ![]() ,
,
∴∠BAC=60°,
∵把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,
∴∠BAE=∠CAE=30°,∠DAF=∠CAF,
∴∠EAP=∠EAC+∠FAC= ![]() BAD=45°,
BAD=45°,
过E作EP⊥AF于P,
此时,PE的值最小,
∵AB=3 ![]() ,∠B=90°,∠BAE=30°,
,∠B=90°,∠BAE=30°,
∴AE=2 ![]() ,
,
∵∠APE=90°,∠EAP=45°,
∴PE= ![]() AE=2
AE=2 ![]() .
.
∴PE的最小值为2 ![]() ,
,
所以答案是:2 ![]() .
.

【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目