题目内容
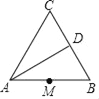
【题目】如图,在等边△ABC中,AB=4,角BAC的平分线交BC于点D,M为AB边中点,N是AD上的动点.
①在图上作出使得BN+MN的和最小时点N的位置,并说明理由.
②求出BN+MN的最小值.(提示:Rt△ABC中,∠C=90°,则有AC2+BC2=AB2成立)
【答案】①详见解析;②BN+MN最小值为2![]() .
.
【解析】
①连接CM,交AD于点N,由题意可得直线AD是等边△ABC的对称轴,即CN=BN,则BN+MN=CN+MN,根据两点之间,线段最短,可得当点N在CM上时,BN+MN最短;
②利用勾股定理可求CM的长度,即可得BN+MN的最小值
解:①如图:连接CM,交AD于点N

∵AD是等边△ABC的角平分线,
∴直线AD是等边△ABC的对称轴
∴BN=CN
∴BN+MN=CN+MN
根据两点之间,线段最短,当点N在线段CM上时,BN+MN最短.
即点N位于CM与AD的交点时,BN+MN最短.
②当点N在CM上时,BN+MN最短,即BN+MN最小值为CM的长度
∵点M是AB的中点
∴AM=BM=2
在Rt△ACM中,CM=![]() =2
=2![]()
∴BN+MN最小值为2![]()

练习册系列答案
相关题目