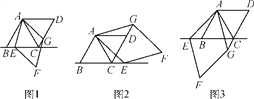
题目内容
【题目】如图,在直角三角形![]() 中,
中,![]() .
.

(1)如图1,点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 有怎样的数量关系,写出你的结论,并加以证明;
有怎样的数量关系,写出你的结论,并加以证明;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上,在线段
的延长线上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
①依题意补全图形;
②若![]() ,求证:
,求证:![]() .
.
【答案】(1)∠ENB=∠NAC,理由见解析;(2)①见解析;②见解析;
【解析】
(1)依据∠NFD=∠ADB=90°,∠ACB=90°,即可得到∠FAC+∠AMC=∠FNC+∠AMC=90°,进而得出∠MAC=∠ENB,再根据∠NAC=∠MAC,即可得到∠ENB=∠NAC;
(2)①过点B作BD⊥AM于点D,过点N作NE∥BD,交BA延长线于点E,交MA延长线于点F;②依据∠ENB=∠NAC,∠NEA=135°-∠ENB,∠EAN=135°-∠NAC,即可得到∠NEA=∠NAE.
(1)∠ENB与∠NAC之间的数量关系:∠ENB=∠NAC,
理由:∵BD⊥AM,
∴∠ADB=90°,
∵NE∥BD,
∴∠NFD=∠ADB=90°,
∵∠ACB=90°,
∴∠FAC+∠AMC=∠FNC+∠AMC=90°,
∴∠MAC=∠ENB,
又∵∠NAC=∠MAC,
∴∠ENB=∠NAC;
(2)①补全图形如图:
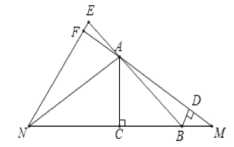
②同理可证∠ENB=∠NAC,
∵在Rt△ABC中,∠ACB=90°,∠CAB=45°,
∴∠ABC=45°,
∴∠ABM=135°,
∴∠NEA=∠ABM∠NEB=135°∠ENB,
∵∠EAN=∠EAB∠NAC∠CAB=135°∠NAC,
∴∠NEA=∠NAE.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目