题目内容
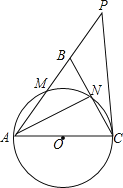
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,直线CP是⊙O的切线,且点P在AB的延长线上.
(1)若∠P=40°,求∠BCP的度数;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
【答案】(1)25°;(2)4
【解析】试题分析:(1)根据CP是⊙O的切线,AC为直径,可得∠ACP=90°,再由∠P=40°从而可得∠BAC=50°,再根据AB=AC求得∠ABC的度数即可得;
(2)作BF⊥AC于F,由题意可得∠ANC=90°,再根据等腰三角形的性质求得CN长,再根据直角三角形两锐角互余推得∠BCP=∠CAN,由已知即可得sin∠CAN=![]() ,从而可得.
,从而可得.
试题解析:(1)∵CP是⊙O的切线,AC为直径,
∴∠ACP=90°,
又∵∠P=40°,
∴∠BAC=50°,
∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BCP =∠ABC-∠P=65°-40°=25°;
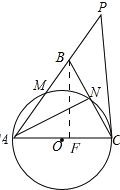
(2)如图,作BF⊥AC于F,
∵AC为直径,
∴∠ANC=90°,
∵AB=AC,
∴CN=![]() CB=
CB=![]() ,
,
∵∠BCP+∠ACN =∠CAN+∠ACN,
∴∠BCP=∠CAN,
∵sin∠BCP=![]() ,
,
∴sin∠CAN=![]() ,
,
∴![]() ,
,
∴AC=5,

练习册系列答案
相关题目