Question

【题目】阅读下列材料，完成相应的学习任务:如图（1）在线段AB上找一点C，C把AB分为AC和BC两条线段，其中AC＞BC．若AC，BC，AB满足关系AC2＝BCAB．则点C叫做线段AB的黄金分割点，这时＝≈0.618，人们把叫做黄金分割数，我们可以根据图（2）所示操作方法我到线段AB的黄金分割点，操作步骤和部分证明过程如下：

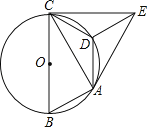
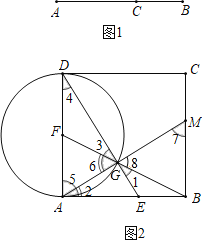
第一步，以AB为边作正方形ABCD．

第二步，以AD为直径作⊙F．

第三步，连接BF与⊙F交于点G．

第四步，连接DG并延长与AB交于点E，则E就是线段AB的黄金分割点．

证明：连接AG并延长，与BC交于点M．

∵AD为⊙F的直径，

∴∠AGD＝90°，

∵F为AD的中点，

∴DF＝FG＝AF，

∴∠3＝∠4，∠5＝∠6，

∵∠2+∠5＝90°，∠5+∠4＝90°，

∴∠2＝∠4＝∠3＝∠1，

∵∠EBG＝∠GBA，

∴△EBG∽△GBA，

∴＝，

∴BG2＝BEAB…

任务：

（1）请根据上面操作步骤与部分证明过程，将剩余的证明过程补充完整；（提示：证明BM＝BG＝AE）

（2）优选法是一种具有广泛应用价值的数学方法，优选法中有一种0.618法应用了黄金分割数．为优选法的普及作出重要贡献的我国数学家是　 　（填出下列选项的字母代号）

A．华罗庚

B．陈景润

C．苏步青

Answer 1

【答案】（1）见解析；（2）A

【解析】

（1）利用相全等三角形的判定和性质、相似三角形的性质以及平行线的性质证明BM=BG=AE即可解决问题．
（2）为优选法的普及作出重要贡献的我国数学家是华罗庚．

（1）补充证明：∵∠2＝∠4，∠ABM＝∠DAE，AB＝AD，

∴△ABM≌△DAE（ASA），

∴BM＝AE，

∵AD∥BC，

∴∠7＝∠5＝∠6＝∠8，

∴BM＝BG＝AE，

∴AE2＝BEAB，

∴点E是线段AB的黄金分割点．

（2）优选法是一种具有广泛应用价值的数学方法，优选法中有一种0.618法应用了黄金分割数．为优选法的普及作出重要贡献的我国数学家是华罗庚．

故答案为A．