Question

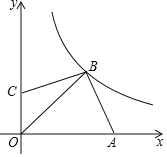
【题目】如图所示平面直角坐标系中，点A，C分别在x轴和y轴上，点B在第一象限，BC＝BA，∠ABC＝90°，反比例函数y＝．（x＞0）的图象经过点B，若OB＝2，则k的值为_____．

Answer 1

【答案】4

【解析】

作BD⊥x轴于D，BE⊥y轴于E，则四边形ODBE是矩形，利用AAS证得△ABD≌△CBE，即可证得BD=BE，然后根据勾股定理求得B的坐标，代入y＝．（x＞0）即可求得k的值．

如图，作BD⊥x轴于D，BE⊥y轴于E，

∴四边形ODBE是矩形，

∴∠DBE＝90°，

∵∠ABC＝90°，

∴∠ABD＝∠CBE，

在△ABD和△CBE中

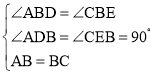
∴△ABD≌△CBE（AAS），

∴BE＝BD，

∴四边形ODBE是正方形，

∵OB＝2，

根据勾股定理求得OD＝BD＝2，

∴B（2，2），

∵反比例函数y＝（x＞0）的图象经过点B，

∴k＝2×2＝4，

故答案为4．