ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯпy= ![]() x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ
x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЎ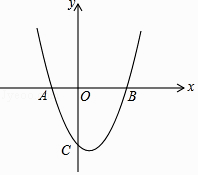
ЃЈ1ЃЉЧѓИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉжБЯпy=Љx+nгыИУХзЮяЯпдкЕкЫФЯѓЯоФкНЛгкЕуDЃЌгыЯпЖЮBCНЛгкЕуEЃЌгыxжсНЛгкЕуFЃЌЧвBE=4ECЃЎ
ЂйЧѓnЕФжЕЃЛ
ЂкСЌНгACЃЌCDЃЌЯпЖЮACгыЯпЖЮDFНЛгкЕуGЃЌЁїAGFгыЁїCGDЪЧЗёШЋЕШЃПЧыЫЕУїРэгЩЃЛ
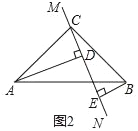
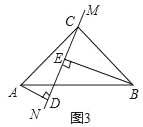
ЃЈ3ЃЉжБЯпy=mЃЈmЃО0ЃЉгыИУХзЮяЯпЕФНЛЕуЮЊMЃЌNЃЈЕуMдкЕуNЕФзѓВрЃЉЃЌЕу MЙигкyжсЕФЖдГЦЕуЮЊЕуM'ЃЌЕуHЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎШєЫФБпаЮOM'NHЕФУцЛ§ЮЊ ![]() ЃЎЧѓЕуHЕНOM'ЕФОрРыdЕФжЕЃЎ
ЃЎЧѓЕуHЕНOM'ЕФОрРыdЕФжЕЃЎ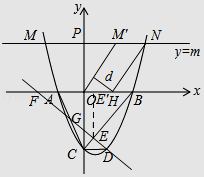
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКЁпХзЮяЯпy= ![]() x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌ
x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌ
Ёр 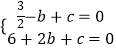 ЃЌНтЕУ
ЃЌНтЕУ 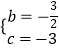 ЃЌ
ЃЌ
ЁрИУХзЮяЯпЕФНтЮіЪНy= ![]() x2Љ
x2Љ ![]() xЉ3ЃЛ
xЉ3ЃЛ
ЃЈ2ЃЉ
НтЃКЂйШчЭМЃЌЙ§ЕуEзїEE'ЁЭxжсгкE'ЃЌдђEE'ЁЮOCЃЌ
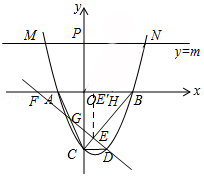
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
ЁпBE=4ECЃЌ
ЁрBE'=4OE'ЃЌ
ЩшЕуEЕФзјБъЮЊЃЈxЃЌyЃЉЃЌдђOE'=xЃЌBE'=4xЃЌ
ЁпBЃЈ2ЃЌ0ЃЉЃЌ
ЁрOB=2ЃЌМДx+4x=2ЃЌ
Ёрx= ![]() ЃЌ
ЃЌ
ЁпХзЮяЯпy= ![]() x2Љ
x2Љ ![]() xЉ3гыyжсНЛгкЕуCЃЌ
xЉ3гыyжсНЛгкЕуCЃЌ
ЁрCЃЈ0ЃЌЉ3ЃЉЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊy=kx+b'ЃЌ
ЁпBЃЈ2ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌ
Ёр ![]() ЃЌНтЕУ
ЃЌНтЕУ 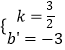 ЃЌ
ЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊy= ![]() xЉ3ЃЌ
xЉ3ЃЌ
ЕБx= ![]() ЪБЃЌy=Љ
ЪБЃЌy=Љ ![]() ЃЌ
ЃЌ
ЁрEЃЈ ![]() ЃЌЉ
ЃЌЉ ![]() ЃЉЃЌ
ЃЉЃЌ
АбEЕФзјБъДњШыжБЯпy=Љx+nЃЌПЩЕУЉ ![]() +n=Љ
+n=Љ ![]() ЃЌ
ЃЌ
НтЕУn=Љ2ЃЛ
ЂкЁїAGFгыЁїCGDШЋЕШЃЎРэгЩШчЯТЃК
ЁпжБЯпEFЕФНтЮіЪНЮЊy=ЉxЉ2ЃЌ
ЁрЕБy=0ЪБЃЌx=Љ2ЃЌ
ЁрFЃЈЉ2ЃЌ0ЃЉЃЌOF=2ЃЌ
ЁпAЃЈЉ1ЃЌ0ЃЉЃЌ
ЁрOA=1ЃЌ
ЁрAF=2Љ1=1ЃЌ
гЩ 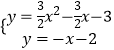 НтЕУ
НтЕУ 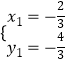 ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
ЁпЕуDдкЕкЫФЯѓЯоЃЌ
ЁрЕуDЕФзјБъЮЊЃЈ1ЃЌЉ3ЃЉЃЌ
ЁпЕуCЕФзјБъЮЊЃЈ0ЃЌЉ3ЃЉЃЌ
ЁрCDЁЮxжсЃЌCD=1ЃЌ
ЁрЁЯAFG=ЁЯCDGЃЌЁЯFAG=ЁЯDCGЃЌ
ЁрЁїAGFЁеЁїCGDЃЛ
ЃЈ3ЃЉ
НтЃКЁпХзЮяЯпЕФЖдГЦжсЮЊx=Љ ![]() =
= ![]() ЃЌжБЯпy=mЃЈmЃО0ЃЉгыИУХзЮяЯпЕФНЛЕуЮЊMЃЌNЃЌ
ЃЌжБЯпy=mЃЈmЃО0ЃЉгыИУХзЮяЯпЕФНЛЕуЮЊMЃЌNЃЌ
ЁрЕуMЁЂNЙигкжБЯпx= ![]() ЖдГЦЃЌ
ЖдГЦЃЌ
ЩшNЃЈtЃЌmЃЉЃЌдђMЃЈ1ЉtЃЌmЃЉЃЌ
ЁпЕу MЙигкyжсЕФЖдГЦЕуЮЊЕуM'ЃЌ
ЁрM'ЃЈtЉ1ЃЌmЃЉЃЌ
ЁрЕуM'дкжБЯпy=mЩЯЃЌ
ЁрM'NЁЮxжсЃЌ
ЁрM'N=tЉЃЈtЉ1ЃЉ=1ЃЌ
ЁпHЃЈ1ЃЌ0ЃЉЃЌ
ЁрOH=1=M'NЃЌ
ЁрЫФБпаЮOM'NHЪЧЦНааЫФБпаЮЃЌ
ЩшжБЯпy=mгыyжсНЛгкЕуPЃЌ
ЁпЫФБпаЮOM'NHЕФУцЛ§ЮЊ ![]() ЃЌ
ЃЌ
ЁрOHЁСOP=1ЁСm= ![]() ЃЌМДm=
ЃЌМДm= ![]() ЃЌ
ЃЌ
ЁрOP= ![]() ЃЌ
ЃЌ
ЕБ ![]() x2Љ
x2Љ ![]() xЉ3=
xЉ3= ![]() ЪБЃЌНтЕУx1=Љ
ЪБЃЌНтЕУx1=Љ ![]() ЃЌx2=
ЃЌx2= ![]() ЃЌ
ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈЉ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрM'ЃЈ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌМДPM'=
ЃЉЃЌМДPM'= ![]() ЃЌ
ЃЌ
ЁрRtЁїOPM'жаЃЌOM'= ![]() =
= ![]() ЃЌ
ЃЌ
ЁпЫФБпаЮOM'NHЕФУцЛ§ЮЊ ![]() ЃЌ
ЃЌ
ЁрOM'ЁСd= ![]() ЃЌ
ЃЌ
Ёрd= ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉИљОнХзЮяЯпy= ![]() x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌПЩЕУХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉЂйЙ§ЕуEзїEE'ЁЭxжсгкE'ЃЌдђEE'ЁЮOCЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌПЩЕУBE'=4OE'ЃЌЩшЕуEЕФзјБъЮЊЃЈxЃЌyЃЉЃЌдђOE'=xЃЌBE'=4xЃЌИљОнOB=2ЃЌПЩЕУx=
x2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉСНЕуЃЌПЩЕУХзЮяЯпЕФНтЮіЪНЃЛЃЈ2ЃЉЂйЙ§ЕуEзїEE'ЁЭxжсгкE'ЃЌдђEE'ЁЮOCЃЌИљОнЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌПЩЕУBE'=4OE'ЃЌЩшЕуEЕФзјБъЮЊЃЈxЃЌyЃЉЃЌдђOE'=xЃЌBE'=4xЃЌИљОнOB=2ЃЌПЩЕУx= ![]() ЃЌдйИљОнжБЯпBCЕФНтЮіЪНЮЊy=
ЃЌдйИљОнжБЯпBCЕФНтЮіЪНЮЊy= ![]() xЉ3ЃЌМДПЩЕУЕНEЃЈ
xЉ3ЃЌМДПЩЕУЕНEЃЈ ![]() ЃЌЉ
ЃЌЉ ![]() ЃЉЃЌАбEЕФзјБъДњШыжБЯпy=Љx+nЃЌПЩЕУnЕФжЕЃЛЂкИљОнFЃЈЉ2ЃЌ0ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌПЩЕУAF=1ЃЌдйИљОнЕуDЕФзјБъЮЊЃЈ1ЃЌЉ3ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌЉ3ЃЉЃЌПЩЕУCDЁЮxжсЃЌCD=1ЃЌдйИљОнЁЯAFG=ЁЯCDGЃЌЁЯFAG=ЁЯDCGЃЌМДПЩХаЖЈЁїAGFЁеЁїCGDЃЛЃЈ3ЃЉИљОнжсЖдГЦЕФаджЪЕУГіOH=1=M'NЃЌНјЖјХаЖЈЫФБпаЮOM'NHЪЧЦНааЫФБпаЮЃЌдйИљОнЫФБпаЮOM'NHЕФУцЛ§ЮЊ
ЃЉЃЌАбEЕФзјБъДњШыжБЯпy=Љx+nЃЌПЩЕУnЕФжЕЃЛЂкИљОнFЃЈЉ2ЃЌ0ЃЉЃЌAЃЈЉ1ЃЌ0ЃЉЃЌПЩЕУAF=1ЃЌдйИљОнЕуDЕФзјБъЮЊЃЈ1ЃЌЉ3ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌЉ3ЃЉЃЌПЩЕУCDЁЮxжсЃЌCD=1ЃЌдйИљОнЁЯAFG=ЁЯCDGЃЌЁЯFAG=ЁЯDCGЃЌМДПЩХаЖЈЁїAGFЁеЁїCGDЃЛЃЈ3ЃЉИљОнжсЖдГЦЕФаджЪЕУГіOH=1=M'NЃЌНјЖјХаЖЈЫФБпаЮOM'NHЪЧЦНааЫФБпаЮЃЌдйИљОнЫФБпаЮOM'NHЕФУцЛ§ЮЊ ![]() ЃЌЧѓЕУOP=
ЃЌЧѓЕУOP= ![]() ЃЌдйИљОнЕуMЕФзјБъЮЊЃЈЉ
ЃЌдйИљОнЕуMЕФзјБъЮЊЃЈЉ ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЕУЕНPM'=
ЃЉЃЌЕУЕНPM'= ![]() ЃЌRtЁїOPM'жаЃЌдЫгУЙДЙЩЖЈРэПЩЕУOM'=
ЃЌRtЁїOPM'жаЃЌдЫгУЙДЙЩЖЈРэПЩЕУOM'= ![]() ЃЌзюКѓИљОнOM'ЁСd=
ЃЌзюКѓИљОнOM'ЁСd= ![]() ЃЌМДПЩЕУЕНd=
ЃЌМДПЩЕУЕНd= ![]() ЃЎ
ЃЎ
ЁОПМЕуОЋЮіЁПИљОнЬтФПЕФвбжЊЬѕМўЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЕФЯрЙижЊЪЖПЩвдЕУЕНЮЪЬтЕФД№АИЃЌашвЊеЦЮедіМѕадЃКЕБa>0ЪБЃЌЖдГЦжсзѓБпЃЌyЫцxдіДѓЖјМѕаЁЃЛЖдГЦжсгвБпЃЌyЫцxдіДѓЖјдіДѓЃЛЕБa<0ЪБЃЌЖдГЦжсзѓБпЃЌyЫцxдіДѓЖјдіДѓЃЛЖдГЦжсгвБпЃЌyЫцxдіДѓЖјМѕаЁЃЎ

 жЧФмбЕСЗСЗВтПМЯЕСаД№АИ
жЧФмбЕСЗСЗВтПМЯЕСаД№АИЁОЬтФПЁПЮЊСЫИќКУИФЩЦКгСїЕФЫЎжЪЃЌжЮЮлЙЋЫООіЖЈЙКТђ10ЬЈЮлЫЎДІРэЩшБИ![]() ЯжгаAЃЌBСНжжаЭКХЕФЩшБИЃЌЦфжаУПЬЈЕФМлИёЃЌдТДІРэЮлЫЎСПШчЯТБэЃКОЕїВщЃКЙКТђвЛЬЈAаЭЩшБИБШЙКТђвЛЬЈBаЭЩшБИЖр2ЭђдЊЃЌЙКТђ2ЬЈAаЭЩшБИБШЙКТђ3ЬЈBаЭЩшБИЩй6ЭђдЊЃЎ
ЯжгаAЃЌBСНжжаЭКХЕФЩшБИЃЌЦфжаУПЬЈЕФМлИёЃЌдТДІРэЮлЫЎСПШчЯТБэЃКОЕїВщЃКЙКТђвЛЬЈAаЭЩшБИБШЙКТђвЛЬЈBаЭЩшБИЖр2ЭђдЊЃЌЙКТђ2ЬЈAаЭЩшБИБШЙКТђ3ЬЈBаЭЩшБИЩй6ЭђдЊЃЎ
AаЭ | BаЭ | |
МлИё | a | b |
ДІРэЮлЫЎСП | 240 | 200 |
![]() ЧѓaЃЌbЕФжЕЃЛ
ЧѓaЃЌbЕФжЕЃЛ
![]() жЮЮлЙЋЫООдЄЫуЙКТђЮлЫЎДІРэЩшБИЕФзЪН№ВЛГЌЙ§105ЭђдЊЃЌФуШЯЮЊИУЙЋЫОгаФФМИжжЙКТђЗНАИЃЛ
жЮЮлЙЋЫООдЄЫуЙКТђЮлЫЎДІРэЩшБИЕФзЪН№ВЛГЌЙ§105ЭђдЊЃЌФуШЯЮЊИУЙЋЫОгаФФМИжжЙКТђЗНАИЃЛ
![]() дк
дк![]() ЕФЬѕМўЯТЃЌШєУПдТвЊЧѓДІРэЮлЫЎСПВЛЕЭгк2040ЖжЃЌЮЊСЫНкдМзЪН№ЃЌЧыФуЮЊжЮЮлЙЋЫОЩшМЦвЛжжзюЪЁЧЎЕФЙКТђЗНАИЃЎ
ЕФЬѕМўЯТЃЌШєУПдТвЊЧѓДІРэЮлЫЎСПВЛЕЭгк2040ЖжЃЌЮЊСЫНкдМзЪН№ЃЌЧыФуЮЊжЮЮлЙЋЫОЩшМЦвЛжжзюЪЁЧЎЕФЙКТђЗНАИЃЎ