题目内容
【题目】(1)探究证明:
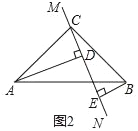
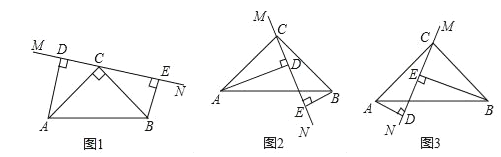
在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E,当直线MN绕点C旋转到图1的位置时,求证:DE=AD+BE;
(2)发现探究:
当直线MN绕点C旋转到图2的位置时,(1)中的结论是否成立,如果不成立,DE、AD、BE应满足的关系是_____.
(3)解决问题:
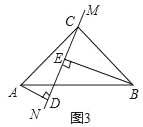
当直线MN绕点C旋转到图3的位置时,若BE=8,AD=2,请直接写出DE的长为_____.

【答案】(1)证明见解析;(2)DE+BE=AD;(3)6.
【解析】试题分析:(1)由垂直得∠ADC=∠BEC=90°,由同角的余角相等得:∠DAC=∠BCE,因此根据AAS可以证明)△ADC≌△CEB,结合全等三角形的对应边相等证得结论;
(2)根据全等三角形的判定定理AAS推知△ACD≌△CBE,然后由全等三角形的对应边相等、图形中线段间的和差关系以及等量代换证得DE+BE=AD;
(3)先同(2)的方法得出DE=BE-AD,代值即可得出结论.
试题解析:证明:(1)如图1.∵AD⊥MN,BE⊥MN,∴∠ADC=∠BEC=90°,∴∠DAC+∠ACD=90°.∵∠ACB=90°,∴∠ACD+∠BCE=90°,∴∠DAC=∠BCE.在△ADC和△CEB中,∵∠ADC=∠BEC,∠DAC=∠BCE,AC=BC,∴△ADC≌△CEB;
∴DC=BE,AD=EC.∵DE=DC+EC,∴DE=BE+AD.
(2)解:(1)中结论不成立,结论为:DE+BE=AD.理由如下:
如图2.∵∠ACB=90°,∴∠ACD+∠BCE=90°.
又∵AD⊥MN于点D,∴∠ACD+∠CAD=90°,∴∠CAD=∠BCE.
在△ADC和△CEB中,∵∠ADC=∠BEC,∠DAC=∠BCE,AC=BC,∴△ADC≌△CEB;
∴CD=BE,AD=CE,∴DE+BE=DE+CD=EC=AD,即DE+BE=AD.
故答案为:DE+BE=AD;
(3)解:如图3,同(2)的方法得,△ADC≌△CEB,∴AD=CE,DC=BE,∴DE=CD﹣CE=BE﹣AD.∵BE=8,AD=2,∴DE=8﹣2=6.故答案为:6.

 阅读快车系列答案
阅读快车系列答案