题目内容
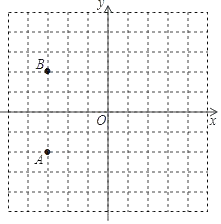
【题目】如图，在直角坐标系中，已知点O，A的坐标分别为（0，0），（﹣3，﹣2）．
（1）点B的坐标是 ，点B与点A的位置关系是 ．现将点B，点A都向右平移5个单位长度分别得到对应点C和D，顺次连接点A，B，C，D，画出四边形ABCD；
（2）横、纵坐标都是整数的点成为整数点，在四边形ABCD内部（不包括边界）的整数点M使S△ABM＝8，请直接写出所有点M的可能坐标；
（3）若一条经过点（0，﹣4）的直线把四边形ABCD的面积等分，则这条直线的表达式是 ，并在图中画出这条直线．
【答案】（1）（﹣3，2），关于x轴对称；（2）点M（1，1），（1，0），（1，﹣1）；（3）y＝﹣8x﹣4
【解析】
（1）根据直角坐标系的特点即可求解，根据题意平移坐标再连接即可；
（2）设△ABM的AB边上的高为h，根据面积求出h，即可求解；
解：（1）B（﹣3，2），A、B关于x轴对称；四边形ABCD如图所示；
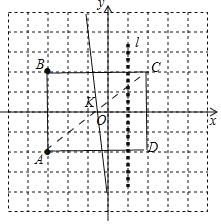
故答案为（﹣3，2），关于x轴对称．
（2）设△ABM的AB边上的高为h，由题意：
×4×h＝8，
∴h＝4，
∴满足条件的点在直线l上，且在矩形内部，
∴点M（1，1），（1，0），（1，﹣1）．
（3）∵直线把四边形ABCD的面积等分，
∴直线经过矩形的对称中心（﹣，0），
设直线的解析式为y＝kx+b，则有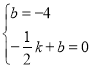
，
解得
，
∴直线的解析式为y＝﹣8x﹣4．
故答案为y＝﹣8x﹣4．
【题目】某学校组织了“热爱宪法，捍卫宪法”的知识竞赛，赛后发现所有学生的成绩（总分100分）均不低于50分，为了解本次竞赛的成绩分布情况，随机抽取若干名学生的成绩作为样本进行整理，并绘制了不完整的统计图表，请你根据统计图表解答下列问题．
学校若干名学生成绩分布统计表
分数段（成绩为x分） | 频数 | 频率 |
50≤x＜60 | 16 | 0.08 |
60≤x＜70 | a | 0.31 |
70≤x＜80 | 72 | 0.36 |
80≤x＜90 | c | d |
90≤x≤100 | 12 | b |
（1）此次抽样调查的样本容量是 ；
（2）写出表中的a＝ ，b＝ ，c＝ ；
（3）补全学生成绩分布直方图；
（4）比赛按照分数由高到低共设置一、二、三等奖，若有25%的参赛学生能获得一等奖，则一等奖的分数线是多少？
