题目内容
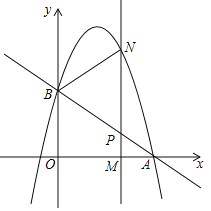
【题目】已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
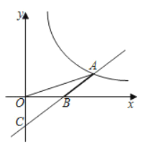
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为
为![]() 轴上一点,
轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
【答案】(1)反比例函数的表达式为![]() ,直线
,直线![]() 的表达式为
的表达式为![]() ;(2)
;(2)![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1) 过点![]() 作
作![]() 轴于
轴于![]() ,根据和
,根据和![]() 求出AD的长度,再利用
求出AD的长度,再利用![]() 和勾股定理得到BD的长度,进而得到答案;
和勾股定理得到BD的长度,进而得到答案;
(2)根据得到的![]() 是等腰三角形分情况
是等腰三角形分情况![]() 、
、![]() 、
、![]() 讨论即可得到答案;
讨论即可得到答案;
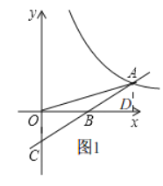
解:(1)如图,过点![]() 作
作![]() 轴于
轴于![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() (勾股定理),
(勾股定理),
∴![]() ,
,
∴![]() ,
,
将点![]() 坐标代入反比例函数
坐标代入反比例函数![]() 中得,
中得,![]() ,
,
∴反比例函数的表达式为![]() ,
,
将点![]() ,
,![]() 代入
代入![]() 中,
中,
得:![]() ,
,
解得: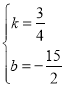
∴直线![]() 的表达式为
的表达式为![]()
(2)由(1)知,![]() ,
,
∵![]() 是等腰三角形,
是等腰三角形,
∴①当![]() 时,
时,
∴![]() ,
,
∴![]() 或
或![]() ,
,
②当![]() 时,如图:
时,如图:
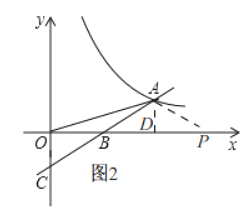
由(1)知,![]() ,
,
易知,点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
③当![]() 时,设
时,设![]() ,
,
∵![]() ,
,![]() ,
,
∴根据两点间的距离公式得到:![]() ,
,![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
即:满足条件的点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:
栽下的各品种树苗棵数统计表 | ||||
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 | |

若经观测计算得出丙种树苗的成活率为89.6%,请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共 棵,乙品种树苗 棵;
(2)图1中,甲 %、乙 %,并将图2补充完整;
(3)求这次植树活动的树苗成活率.
【题目】复课返校后,为了让同学们进一步了解“新型冠状病毒”的防控知识,某学校组织了一次关于“新型冠状病毒”的防控知识比赛,从问卷中随机抽查了一部分,对调查结果进行了分组统计,并制作了如下表格与条形统计图:
分组结果 | 频数 | 频率 |
A.完全掌握 | 30 | 0.3 |
B.比较清楚 | 50 |
|
C.不怎么清楚 |
| 0.15 |
D.不清楚 | 5 | 0.05 |
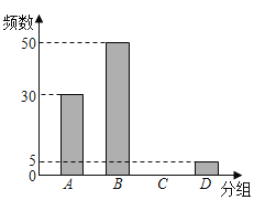
请根据上图完成下面题目:
(1)总人数为 人,![]() ,
,![]() ;
;
(2)请你补全条形统计图;
(3)若全校有2700人,请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少.