题目内容
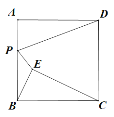
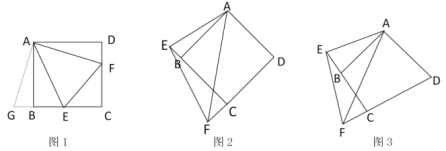
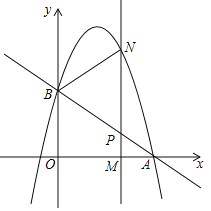
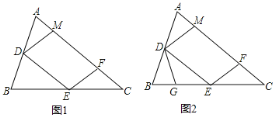
【题目】如图1,锐角△ABC中,D、E分别是AB、BC的中点,F是AC上的点,且∠AFE=∠A,DM//EF交AC于点M.
(1)求证:DM=DA;
(2)点G在BE上,且∠BDG=∠C,如图2,
① 求证:△DEG∽△ECF;
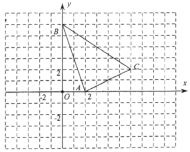
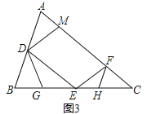
② 从线段CE上取一点H,连接FH使∠CFH=∠B,若BG=1,求EH的长.
【答案】(1)见解析 (2)①见解析 ②1
【解析】
(1)根据平行线性质得∠AMD=∠AFE,可证∠AMD=∠A,得DM=DA;
(2)①根据三角形中位线性质得DE∥AC,证∠DEG=∠C,∠GDE=∠FEC,可证△DEG∽△ECF;
②证△BDG∽△BED,得![]() ,BD2=BGBE;证△EFH∽△ECF,得
,BD2=BGBE;证△EFH∽△ECF,得![]() ,EF2=EHEC,又可证四边形DEFM是平行四边形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
,EF2=EHEC,又可证四边形DEFM是平行四边形,故EF=DM=DA=BD,所以BGBE=EHEC,又BE=EC,故EH=BG.
解:(1)证明:如图1所示,
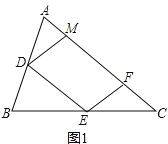
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)①证明:如图2所示,
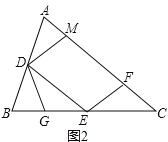
∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
②如图3所示,
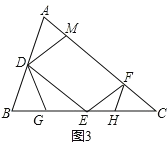
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴![]() ,
,
∴BD2=BGBE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°-∠A-∠B=180°-∠AFE-∠CFH=∠EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴![]() ,
,
∴EF2=EHEC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BGBE=EHEC,
∵BE=EC,
∴EH=BG=1.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案【题目】在“3.15”植树节活动后,对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分:
栽下的各品种树苗棵数统计表 | ||||
植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
植树棵数 | 150 | 125 | 125 | |

若经观测计算得出丙种树苗的成活率为89.6%,请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共 棵,乙品种树苗 棵;
(2)图1中,甲 %、乙 %,并将图2补充完整;
(3)求这次植树活动的树苗成活率.