题目内容
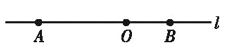
【题目】如图，半圆O的直径AB=4，P，Q是半圆O上的点，弦PQ的长为2，则 
与 
的长度之和为（ ）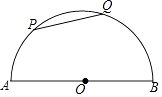 
A.
B.
C.
D.π
【答案】B
【解析】解：如图，连接OP、OQ，则OP=OQ=2，
∵OP=OQ=PQ=2，
∴△OPQ为等边三角形，
∴∠POQ=60°，
∴∠AOP+∠BOQ=120°，
则 
与 
的长度之和为 
= 
，
故选：B．
【考点精析】利用垂径定理和弧长计算公式对题目进行判断即可得到答案，需要熟知垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧；若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的．
练习册系列答案
相关题目
【题目】某校开展了“让世界充满爱”的捐款助学活动，其中八(2)班全体同学的捐款情况如下表：
捐款金额(元) | 5 | 10 | 15 | 20 | 50 |
捐款人数(人) | 7 | 18 | 12 | 3 |
由于填表的同学不小心把墨水滴在了表上，致使表中数据不完整，但知道捐款金额为10元的人数为全班人数的36%，结合上表回答下列问题：
(1)八(2)班共有多少人？
(2)学生捐款金额的众数和中位数分别为多少元？
(3)如果把该班学生的捐款情况绘制成扇形统计图，则捐款金额为20元的人数所对应的扇形圆心角为多少度？
