题目内容
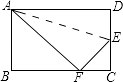
【题目】如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C. 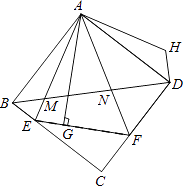
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3 ![]() ,求AG、MN的长.
,求AG、MN的长.
【答案】
(1)证明:∵△AEB由△AED翻折而成,
∴∠ABE=∠AGE=90°,∠BAE=∠EAG,AB=AG,
∵△AFD由△AFG翻折而成,
∴∠ADF=∠AGF=90°,∠DAF=∠FAG,AD=AG,
∵∠EAG+∠FAG=∠EAF=45°,
∴∠ABE=∠AGE=∠BAD=∠ADC=90°,
∴四边形ABCD是矩形,
∵AB=AD,
∴四边形ABCD是正方形
(2)解:MN2=ND2+DH2,
理由:连接NH,
∵△ADH由△ABM旋转而成,
∴△ABM≌△ADH,
∴AM=AH,BM=DH,
∵由(1)∠BAD=90°,AB=AD,
∴∠ADH=∠ABD=45°,
∴∠NDH=90°,
∵ 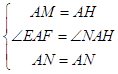 ,
,
∴△AMN≌△AHN,
∴MN=NH,
∴MN2=ND2+DH2
(3)解:设AG=BC=x,则EC=x﹣4,CF=x﹣6,
在Rt△ECF中,
∵CE2+CF2=EF2,即(x﹣4)2+(x﹣6)2=100,x1=12,x2=﹣2(舍去)
∴AG=12,
∵AG=AB=AD=12,∠BAD=90°,
∴BD= ![]() =
= ![]() =12
=12 ![]() ,
,
∵BM=3 ![]() ,
,
∴MD=BD﹣BM=12 ![]() ﹣3
﹣3 ![]() =9
=9 ![]() ,
,
设NH=y,
在Rt△NHD中,
∵NH2=ND2+DH2,即y2=(9 ![]() ﹣y)2+(3
﹣y)2+(3 ![]() )2,解得y=5
)2,解得y=5 ![]() ,即MN=5
,即MN=5 ![]() .
.
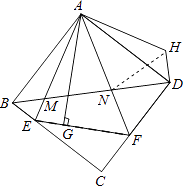
【解析】(1)由图形翻折变换的性质可知∠ABE=∠AGE=∠BAD=∠ADC=90°,AB=AD即可得出结论;(2)连接NH,由△ABM≌△ADH,得AM=AH,BM=DH,∠ADH=∠ABD=45°,故∠NDH=90°,再证△AMN≌△AHN,得MN=NH,由勾股定理即可得出结论;(3)设AG=x,则EC=x﹣4,CF=x﹣6,在Rt△ECF中,利用勾股定理即可得出AG的值,同理可得出BD的长,设NH=y,在Rt△NHD,利用勾股定理即可得出MN的值.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案【题目】某市实行中考改革,需要根据该市中学体能的实际情况重新制定中考体育标准.为此,抽取了50名初中毕业的女学生进行“一分钟仰卧起坐”次数测试.测试的情况绘制成表格如下:
(1)求这次抽样测试数据的平均数、众数和中位数;
(2)根据这一样本数据的特点,你认为该市中考女生“一分钟仰卧起坐”项目测试的合格标准应定为多少次较为合适?请简要说明理由;
(3)根据(2)中你认为合格的标准,试估计该市中考女生“一分钟仰卧起坐”项目测试的合格率是多少?
次数 | 6 | 12 | 15 | 18 | 20 | 25 | 27 | 30 | 32 | 35 | 36 |
人数 | 1 | 1 | 7 | 18 | 10 | 5 | 2 | 2 | 1 | 1 | 2 |