Question

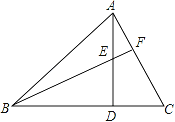
【题目】如图，在△ABC中，AD⊥BC于D，BF与AD相交于E．若AD=BD，BE=AC，BC=8cm，DC=3cm，则AE=_____，∠BFC=_____．

Answer 1

【答案】2cm 90°

【解析】

由题意可得BD=AD=5cm，根据已知可证明△BDE≌△ADC（HL），可得DE=CD=3cm，根据AE=AD-DE求出AE长即可，根据∠DAC+∠C=90°，∠DAC=∠DBE可得∠DBE+∠C=90°，即可求出∠BFC=90°.

∵BC=8cm，DC=3cm，

∴BD=AD=5cm，

在Rt△BDE和Rt△ADC中，

∵BE=AC，BD=AD，

∴△BDE≌△ADC（HL），

∴DE=CD=3cm，∠DAC=∠DBE，

∴AE=AD-DE=5-3=2cm，

∵∠DAC+∠C=90°，∠DAC=∠DBE，

∴∠DBE+∠C=90°，

∴∠BFC=90°

故答案为：(1).2cm；(2). 90°