Question

【题目】已知△ABC为等边三角形，点D为直线BC上一动点（点D不与B，C重合），以AD为边作菱形ADEF（A，D，E，F按逆时针排列），使∠DAF=60°，直线EF与直线BC交于H.

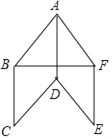
（1）如图①，当点D在边BC上时，试说明：；

（2）如图②，当点D在边BC的延长线上且其他条件不变时，结论；是否成立？若成立，请说明理由；若不成立，请写出AD、DH、AC之间存在的数量关系；

（3）如图③，当点D在边CB的延长线上且其他条件不变时，补全图形，并直接写出AD、DH、AC之间存在的数量关系.

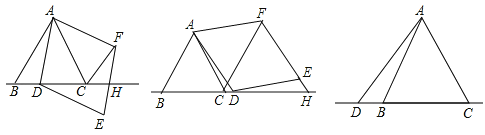
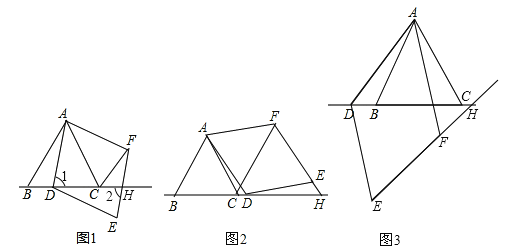
图1 图2 图3

Answer 1

【答案】（1）证明见解析；（2）成立；（3）补图见解析，数量关系.

【解析】分析：（1）通过△ACD∽△DEH的对应边成比例得到，即=，则AD2=DHAC；

（2）图（2）中，AD2=DHAC仍然成立．易证△ACD∽△DEH，则该相似三角形的对应边成比例：，即=，则AD2=DHAC；

（3）如图3，解题思路同（2）．易证△ACD∽△DEH，则该相似三角形的对应边成比例：，即=，则AD2=DHAC．

详解：（1）∵四边形ADEF是菱形，∠DAF=60°，

∴AD∥EF，∠DAF=∠E=60°，AD=DE，∴∠1=∠2．

∵△ABC是等边三角形，∴∠ACD=60°，∠ACD=∠E，∴△ACD∽△DEH，∴，即=，∴AD2=DHAC；

（2）结论是：图（2）中，AD2=DHAC仍然成立．

理由如下：如图2．

∵在菱形ADEF中，AD∥EF，∠DAF=∠E=60°，AD=DE，∴∠ADC=∠DHE，∠DEF=120°．

又∵△ABC是等边三角形，∴∠ACB=60°，∴∠ACD=120°，∴∠ACD=∠DEH，∴△ACD∽△DEH，∴，即=，则AD2=DHAC；

（3）补全图形是如图3．数量关系AD2=DHAC．理由同（2）．