题目内容
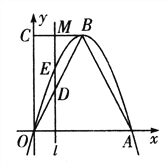
【题目】如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在上.
(1)求∠AED的度数;
(2)若⊙O的半径为2,则的长为多少?
(3)连接OD,OE,当∠DOE=90°时,AE恰好是⊙O内接正n边形的一边,求n的值.

【答案】(1) 120°;(2)![]() ;(3)12
;(3)12
【解析】试题分析:(1)连接AC,由AB=AD可得到∠ACB=∠ACD=60°,在四边形ACBE中由对角互补可求得∠AEB,(2)因为 ∠AOD=2∠ABD=120°,半斤为2,根据弧长公式即可求解.
(3)连接OA,求出∠AOE的度数即可求出正n边形的边数.
连接BD,∵四边形ABCD是 O的内接四边形,
∴∠BAD+∠C=180°,
∵∠C=120°,
∴∠BAD=60°,
∵AB=AD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∵四边形ABDE是 O的内接四边形,
∴∠AED+∠ABD=180°,
∴∠AED=120°,
(2) ∵∠AOD=2∠ABD=120°,
∴弧AD的长=![]() ,
,
(3)连接OA,
∵∠ABD=60°,
∴∠AOD=2∠ABD=120°,
∵∠DOE=90°,
∴∠AOE=∠AOD-∠DOE=30°,
∴n=![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目