题目内容
【题目】如图,已知平行四边形ABCD延长BA到点E,延长DC到点E,使得AE=CF,连结EF,分别交AD、BC于点M、N,连结BM,DN.
(1)求证:AM=CN;
(2)连结DE,若BE=DE,则四边形BMDN是什么特殊的四边形?并说明理由.
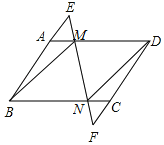
【答案】(1)见解析;(2)四边形BMDN是菱形,理由见解析.
【解析】
(1)由题意可证△AEM≌△FNC,可得结论.
(2)由题意可证四边形BMDN是平行四边形,由题意可得BE=DE=DF,即可证∠BEM=∠DEF,即可证△BEM≌△DEM,可得BM=DM,即可得结论.
(1)∵四边形ABCD是平行四边形
∴AB∥CD,AD∥BC,∠BAD=∠BCD
∴∠E=∠F,∠EAM=∠FCN
∵∠E=∠F,∠EAM=∠FCN,AE=CF
∴△AEM≌△CFN
∴AM=CN
(2)菱形
如图
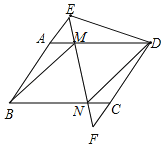
∵AD=BC,AM=CN
∴MD=BN且AD∥BC
∴四边形BMDN是平行四边形
∵AB=CD,AE=CF
∴BE=DF,且BE=DE
∴DE=DF
∴∠DEF=∠DFE
且∠BEF=∠DFE
∴∠BEF=∠DEF,且BE=DE,EM=EM
∴△BEM≌△EMD
∴BM=DM
∵四边形BMDN是平行四边形
∴四边形BMDN是菱形.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目