题目内容
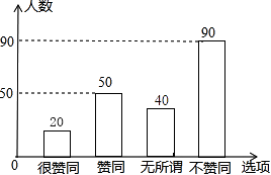
【题目】某校八年级数学兴趣小组的同学调查了若干名家长对“初中生带手机上学”现象的看法,统计整理并制作了如下的条形与扇形统计图.依据图中信息,解答下列问题: 
(1)接受这次调查的家长共有人;
(2)补全条形统计图;
(3)在扇形统计图中,“很赞同”的家长占被调查家长总数的百分比是;
(4)在扇形统计图中,“不赞同”的家长部分所对应扇形的圆心角度数是度.
【答案】
(1)200
(2)解:
(3)10%
(4)162
【解析】解:(1.)本次调查的学生家长有 ![]() =200(名), 无所谓的人数是:200×20%=40(人),
=200(名), 无所谓的人数是:200×20%=40(人),
很赞同的人数是:200﹣50﹣40﹣90=20(人),
所以答案是200人.
(2.)根据(1)求出的无所谓的人数是40,很赞同的人数是20补图如下:
(3.) ![]() ×100%=10%.
×100%=10%.
所以答案是10%.
(4.)“不赞同”的家长部分所对应扇形的圆心角度数360°× ![]() =162°,
=162°,
所以答案是162.
【考点精析】本题主要考查了扇形统计图和条形统计图的相关知识点,需要掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能正确解答此题.

 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | 4 | 1 | 0 | 1 | 4 | … |
点A(x1,y1)、B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,y1与y2的大小关系正确的是( )
A.y1>y2B.y1<y2C.y1≥y2D.y1≤y2
【题目】已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC | A(a,0) | B(3,0) | C(5,5) |
△A′B′C′ | A′(4,2) | B′(7,b) | C′(c,7) |
(1)观察表中各对应点坐标的变化,并填空:a= , b= , c=;
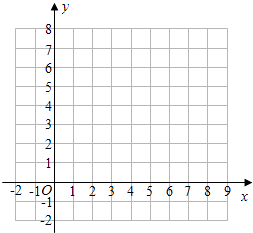
(2)在平面直角坐标系中画出△ABC及平移后的△A′B′C′;
(3)直接写出△A′B′C′的面积是 .