题目内容
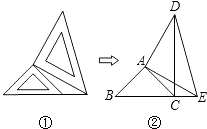
【题目】将一副三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.
【答案】
(1)证明:∵CF平分∠DCE,
∴∠1=∠2= ![]() ∠DCE,
∠DCE,
∵∠DCE=90°,
∴∠1=45°,
∵∠3=45°,
∴∠1=∠3,
∴AB∥CF(内错角相等,两直线平行);
(2)解:∵∠D=∠B=∠C
∴∠DFC=180°﹣30°﹣45°=105°.
【解析】一副三角板的特征是一个是等腰直角三角形,一个是含30°、60°直角三角形,由内错角法可判定两直线平行,由内角和定理求出∠DFC.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对平行线的判定的理解,了解同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目