题目内容
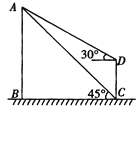
【题目】为了测量某风景区内一座塔AB的高度,某人分别在塔的对面一楼房CD的楼底C、楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度。(结果精确到0.1m)(参考数据![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】AB≈23.7米
【解析】
过点D作DE⊥AB,设AB=x,则BC=x,根据矩形可得BE=CD=10,则AE=10-x,根据Rt△ADE中tan∠ADE的值求出x的值.
设AB=x,过点D作DE⊥AB,垂足为E,得矩形BCDE
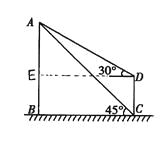
∴BE=CD=10,DE=BC, ∴AE=x-10 在Rt△ABC中,∵∠ACB=45°,∠B=90°
∴∠ACB=∠BAC=45° ∴BC=AB=x
∴在Rt△AED中, ∵∠ADE=30°,DE=BC=x,tan∠ADE=![]() , ∴
, ∴![]()
∴x=15+5![]() ≈23.7(m)
≈23.7(m)
答:塔AB的高度约为23.7m.

练习册系列答案
相关题目