题目内容
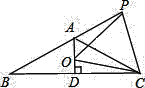
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,D为BC上一点,过点D作DE⊥AB于E.
(1)连接AD,取AD中点F,连接CF,CE,FE,判断△CEF的形状并说明理由
(2)若BD=![]() CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.
CD,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,求出n的值.

【答案】(1)等边三角形,理由见解析(2) n=60°或135°.
【解析】
(1)根据直角三角形斜边的中线等于斜边的一半证得FC=FE即可,再证明∠CFE=60°,从而进行判断;
(2)根据∠B=60°,∠DEB=90°,可知BD=![]() DE,又BD=
DE,又BD=![]() CD,则DC=DE,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,∠BDB'等于旋转角,分两种情况求解即可..
CD,则DC=DE,将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边上时,∠BDB'等于旋转角,分两种情况求解即可..
(1)∵∠ACB=90°,F是AD中点,
∴FC=![]() AD,
AD,
∵DE⊥AB,F是AD中点,
∴EF=![]() AD,
AD,
∴FC=FE,
∴△CEF是等腰三角形;
又EF=AF,CF=AF,故∠CFE=2∠CAB=60°
从而可知:△CEF是等边三角形.
(2)n=60°或135°
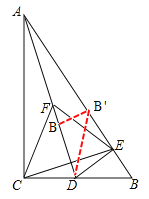
理由:①将△BED绕着点D逆时针旋转n°(0<n<180),当点B落在Rt△ABC的边AC上时,此时记为B'点,

△B'CD为直角三角形,
又∵BD=![]() CD,
CD,
故∠B'DC=45°;从而旋转角∠BDB'=180°-∠B'DC=180°-45°=135°
②当B'在边AB上时,有DB=DB',又∠B=60°,故可知△DBB'为等边三角形,所以∠BDB'=60°;即n=60°

【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.